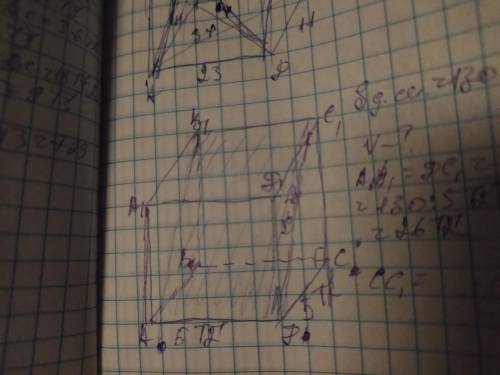
В основе правильной четырёхугольной призме лежит квадрат. Диагональным сечением призмы является прямоугольник, и так как известна его площадь, найдём его вторую сторону по формуле обратной формуле площади:
АВ1=ДС1=130÷5√2=26√2см
Вторая сторона диагонального сечения также является диагональю в гранях АА1В1В и ДД1С1С. Диагональ делит эти грани на 2 равных прямоугольных треугольника, в которых сторона основания и высота призмы являются катетами а диагональ гипотенузой. Зная сторону и диагональ найдём высоту призмы по теореме Пифагора:
ДД1²=С1Д²-СД2=(26√2)²-(5√2)²=
=676×2-25×2=1352-50=1302; ДД1=√1302см
Теперь найдём объем призмы, зная стороны и высоту по формуле:
V=а²×h, где а- стороны основания, а h-высота призмы:
V=(5√2)²×√1302=25×2×√1302=
=50√1302см³
ОТВЕТ: V=50√1302см³
Объяснение:
1. Пусть бок сторона А (это меньшая сторона), длина или основание В,
каждая биссектриса образует равнобедренный треугольник со стороной А, т.е. В делится на три равные части сумма двух из них равна А
Вывод В = 1,5 А или А = 2/3 В
2. у треугольников, куда входят стороны указанные пунктиром равные другие стороны (длины сторон пар-ма у каждого), осталось доказать что углы между ними тоже равны, помня что у равнобедренных = 60, а у пар-ма противополож равны, а смежные в сумме дают 180 ...
т.е у двоих а+60, а у третьего 360 - (180 - а) - 120 = 60 + а, т.е треугольники равны ...