Дотична пряма до кола в евклідовій геометрії на площині — пряма, що дотикається до кола тільки в одній точці та не містить внутрішніх точок кола. Грубо кажучи, це пряма, яка проходить через пару нескінченно близьких точок на колі. Дотичні прямі до кола застосовуються у багатьох геометричних побудовах і доведеннях. Так як, дотична пряма до кола є перпендикуляром до радіуса кола, проведеного в точку дотику, то зазвичай теореми в яких розглядаються дотичні прямі, часто використовують у формулюванні такі радіуси або ортогональні кола.
Уравнение АВ: (x-(-3))/(5-(-3) = (y-3)/(-1-3) или (x + 3)/8 = (y - 3)/(-4).
В общем виде x + 2y - 3 = 0.
Так как высота АД - горизонтальная линия, то уравнение стороны ВС:
х = 5.
В уравнении высоты СД как перпендикуляра к АВ коэффициенты А и В меняются на -В и А (скалярное произведение равно 0).
Уравнение СД: -2х + у + С = 0. Подставим координаты точки Д, через которую проходит высота: -2*4 + 1*3 + С = 0, отсюда С = 8-3 = 5.
Уравнение СД: -2х + у + 5 = 0.
Находим координаты точки С как точки пересечения стороны ВС и высоты СД:
{x = 5,
{-2х + у + 5 = 0, подставим х = 5.
-2*5 + у + 5 = 0, у = 10 - 5 = 5.
Точка С(5;5).
Уравнение АС: (x-(-3))/(5-(-3) = (y-3)/(5-3) или (x + 3)/8 = (y - 3)/2.
В общем виде x - 4y + 15 = 0.
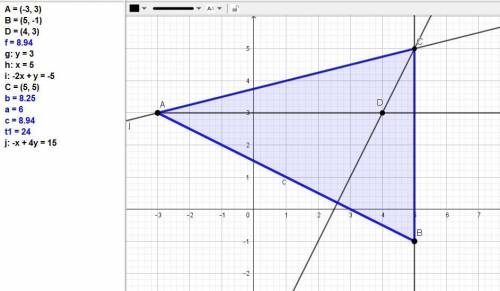
Это быть не может, значит такого треугольника не существует!