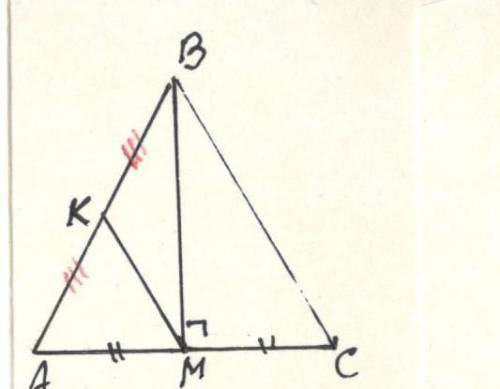
Отрезок BM — медиана равнобедренного треугольника ABC (AB=BC). На стороне AB отметили точку К такую, что КМ параллельно BC. Докажите, что BK=КМ.
Дано :
AB = BC (боковые стороны)
AM = MC ( BM медиана)
КМ || BC ( К ∈ [AB] )
- - - - - - -
Док- ать BK = KM
Объяснение:
AM = MC и КМ || BC ⇒ (т. Фалеса ) AK = BK = AB/2 = BC/2
следовательно КM средняя линия треугольника ABC
КM = BC/ 2 но и BK = BC / 2 ⇒ BK = KM ч.т.д.
Можно и по другому (2 -ой В прямоугольном треугольнике AMB (∠AMB =90° , AB _гипотенуза медиана BM треугольника ABC одновременно и высота ) медиана MK = AB/2 (половине гипотенузы) = BK.
рис. cм ПРИЛОЖЕНИЕ
26 - 2*5 = 16 (cм) - длина сторон-оснований.
16/2 = 8 (см) - длина средней линии.
ответ
ответ разместил: Гость
Все довольно таки просто: если угол Д=30⁰, а гипотенуза ΔАСД 24 см, то сторона АС в данном треугольнике равна половине гипотенузы, т.е. АС=½АД=24/2=12 см. Сторона АС в Δ АВС является гипотенузой, а угол ВАС равен 90-60=30⁰ ( поясняю: треугольник АСД прямоугольный, угол Д по условию 30⁰, значит угол САД равен 90-30=60⁰. Угол А по условию 90⁰, а высота АС делит его на 2 угла, один из которых 60⁰), значит ВС=½АС=12/2=6 см. ответ:6 смответ:
Объяснение:
1. Находим координаты точки В, взяв отрезок АВ и его середину М.
х=2·3-(-1)=6+1=7
у=2·4-3=8-3=5
В(7;5)
2. Находим координаты точки С, взяв отрезок ВС и его середину N.
х=2·4-7=8-7=1
у=2·2-5=4-5=-1
С(1;-1)
3. Находим длины медиан по формуле расстояния между точками.
АN²=(4+1)²+(2-3)²=25+1=26
АN=√26
СМ²=(3-1)²+(4+1)²=4+25=29
СМ=√29