Свойства параллельных плоскостей
Рассмотрим два свойства параллельных плоскостей.
1°. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Наглядным подтверждением этого факта служат линии пересечения пола и потолка со стеной комнаты — эти линии параллельны.
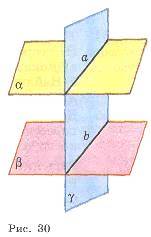
Для доказательства данного свойства рассмотрим прямые а и b, по которым параллельные плоскости α и β пересекаются с плоскостью γ (рис. 30). Докажем, что прямые а и b параллельны. Эти прямые лежат в одной плоскости (в плоскости γ) и не пересекаются. В самом деле, если бы прямые а и b пересекались, то плоскости α и β имели бы общую точку, что невозможно, так как эти плоскости параллельны.
Итак, прямые а и b лежат в одной плоскости и не пересекаются, т.е. прямые а и b параллельны.
2°. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Для доказательства этого свойства рассмотрим отрезки АВ и CD двух параллельных прямых, заключенные между параллельными плоскостями α и β (рис. 31). Докажем, что AB=CD. Плоскость γ, проходящая через параллельные прямые АВ и CD, пересекается с плоскостями α и β по параллельным прямым АС и BD (свойство 1°). Таким образом, в четырехугольнике ABDC противоположные стороны попарно параллельны, т.е. ABDC — параллелограмм. Но в параллелограмме противоположные стороны равны, поэтому отрезки АВ и CD равны.
а = 3, в = 4, с = 5. Треугольник прямоугольный, т.к 5² =3² + 4²
Биссектриса внутреннего угла тр-ка делит противолежащую углу сторону на части, пропорциональные прилегающим сторонам, т.е гипотенуза с поделена на отрезки: х, прилегающий к стороне а и (с-х), прилегающий к стороне b.
а:a1 = b:b1
3:х = 4:(5-x)
15 - 3x = 4x
7x = 15
a1 = x = 15/7
b1 = 5-x = 5 - 15/7 = 20/7
Сама биссектриса равна:
Lc = √(a·b - a1·b1)
Lc = √(3·4 - 15/7· 20/7)= √(12 - 300/49) = √(588/49 - 300/49) = √(288/49) =
12√2/7
ответ: 12
L AED = 15 град.
L D = L B = 150 град. =>
L DAE = 180 - (L AED + L D) = 180 - (15 + 150) = 15 град. =>
треугольник ADE - равнобедренный =>
AD = DE = DC - EC = AB - EC = 7 - 3 = 4 см
2) СК - высота из С на продолжение стороны АВ.
Треугольник CKB:
BC = AD = 4 см
L CBK = 180 - L ABC = 180 - 150 = 30 град. =>
CK = 1/2 * BC = 1/2 * 4 = 2 см - высота трапеции =>
3) S (ABCD) = AB * CK = 7 * 2 = 14 см^2