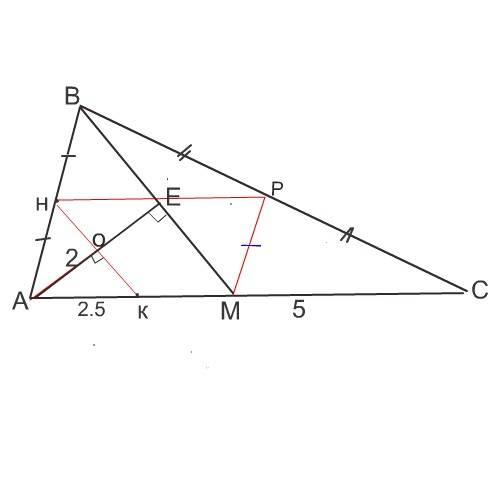
Сделаем рисунок к задаче, стараясь придерживаться заданных в ней пропорций.
Обозначим середины АВ и ВС как Н и Р соответственно. Проведем отрезок НР - среднюю линию треугольника АВС.
Обозначим точку К - середину АМ.
Соединим середины АВ и АМ отрезком НК.
НК параллельна ВМ как средняя линия треугольника АВМ и, соответственно, равна половине медианы ВМ.
Рассмотрим треугольник АКО. В нем АО перпендикулярна КН, т.к. АЕ - расстояние от А до ВМ определяется отрезком, перпендикулярным ВМ.
Поскольку КН параллельна ВМ, то АО перпендикулярна КН.
Из треугольника АОК, в котором АО=половине АЕ, а АК - половине АМ,
по теореме Пифагора найдем ОК.
ОК=√(2,5²-2²)=1,5 см
КН=2 ОК=3 см
ВМ=2КН=6 см
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, является высотой этой трапеции и делит это основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности. ⇒ Средняя линия этой трапеции – 22. Подробное решение: Если опустить еще один перпендикуляр из вершины второго угла при меньшем основании, получим разделенное на 3 части основание, две из которых равны по 15 ( у каждого острого угла при основании), а третья, средняя, равна меньшему основанию и равна
22-15=7.
Длина меньшего основания равна 7,
большего основания равна
22+15=37 .
Сумма длин оснований равна
37+7=44
Средняя линия трапеции равна полусумме оснований и равна
44:2=22