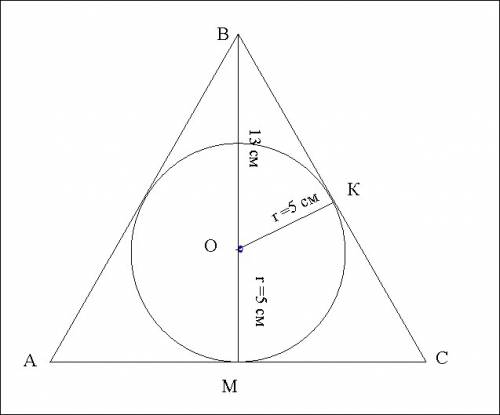
Дано: ΔАВС
АВ=ВА
(О; r) - вписанная окр.
ВМ⊥АС
ВО=13 см
ОК= r = 5 см
Найти: Р ΔАВС
1) Из прямоугольного ΔВОК по теореме Пифагора
ВК² = ВО² - ОК²
ВК² = 13²- 5² =169-25=144
ВК=√144 = 12 см
2) ∆ОВК~∆МВС (подобен), т.к. оба прямоугольные с общим углом ∠МВС.
Соответственные стороны пропорциональны:
ВМ : МС = ВК : ОК
18 : МС = 12 : 5
МС =18 · 5:12 = 7,5 см
АС = 2 · МС = 2·7,5 = 15 см.
3) По теореме Пифагора из ∆ВМС найдем ВС.
ВС² = ВМ² + МС²
ВС² = 18² + 7,5² = 324 + 56,25 = 380,25
ВС=√380,25 = 19,5 см
4) АВ = ВС = 19,5 см
АС = 15 см
Р= АВ+ВС+АС
Р = 2*19,5 + 15 = 54 см
ответ: 54 см
Площадь полной поверхности призмы равна:
Sп.п. =2* S ΔABC +Sб.п.
SΔABC=6*8/2=24(см²)
Sб.п.=S AA₁B₁B+S CC₁B₁B+S ACC₁A₁
АС²=AB²+BC² по теореме Пифагора
АС²=36+64=100(см²)
АС= √100 =10(см)
Sб.п.=6*7+8*7+10*7=42+56+70=168(см²)
Sп.п. =2*24+168=48+168=216(см²)
образующая конуса =7,5 см, высота 6 см. находим объем конуса V конуса=(1/3)Sоснования*h.
r основания по теореме Пифагора=4,5.
S основания= r^2= 20,25
V конуса=(1/3)20,25*6=40,5.