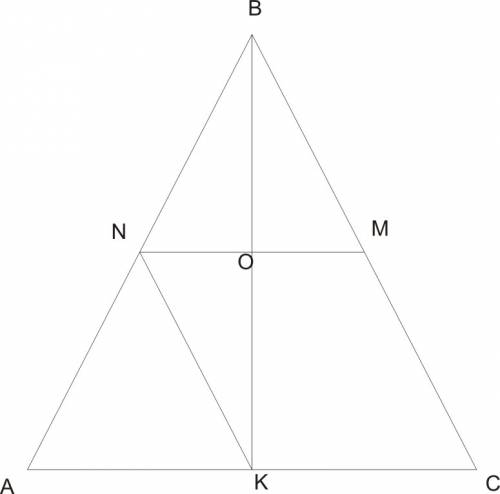
Δ АВС - равнобедренный
ВК = 30 см - биссектриса к основанию АС, она же и медиана Δ АВС ⇒ АК=КС
NM = 16 см - средняя линия II АС ⇒AN=NB
NK = ? - средняя линия II ВС
NM x ВК в т.О и деляться ей пополам, т.к. Δ NMB подобен Δ АВС по 3-м углам, ⇒ Δ NMB равнобедренный и ВО его высота, биссектриса и медиана.
ВО=ВК т.к. NM средняя линия Δ АВС
Получаем
NO=1/2NM= 16/2=8
OK=1/2ВК= 30/2=15
Δ NOK прямоугольный, т.к. уже доказано, что BO высота Δ NMB ⇒ <BON = 90°
<NOK - смежный и =180°-<BON = 90°
По теореме Пифагора находим NK - гипотенузу Δ NOK
NK=√(NO²+OK²) = √(8²+15²)=√(64+225)=√289=17 см
Мне решили на этом сайте очень хороший человек,думаю это решение и тебе пригодиться:)поблагодарить можешь ellagabdullina
По теореме Пифагора найдем в нем гипотенузу ВС.
ВС^2 = 24^2 + 18^2 = 576 + 324 = 900
ВC = корень из 900 = 30
Воспользуемся свойством пропорциональных отрезков в прямоугольном треугольнике АВС.
ВД = под корнем СД*АД
24 = под корнем 18 *АД
24^2 = 18*АД
576 = 18АД
АД = 576 : 18 = 32
Тогда АС = 32+18 = 50
В прямоуг. треугольнике АВС найдем катет АВ по теореме Пифагора
АB^2 = 50^2 - 30^2 = 2500 - 900 = 1600/ Тогда АВ = корень из 1600 = 40(см)
cos A = AB/AC = 40/50 = 4/5 = 0,8
ответ: АВ = 40 см; cos А = 0,8
3х=9
х=9/3
х=3