Объяснение:
В треугольнике против меньшей стороны лежит меньший угол.Пусть а = 14 см, b=16 см и c=18 см
a - меньшая сторона. Ищем угол α по теореме косинусов
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.Формула теоремы косинусов:
a² = b² + c² - 2bc cos α
14²=16²+18²-2*16*18* cos α
196=256+324-576*cos α
576*cos α=384
cos α=384/576=2/3≅0,667
По таблице косинусов найдём приблизительное значение угла α:
∠α≅48°
Объяснение:
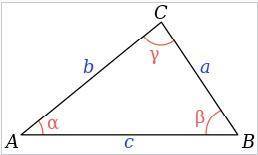
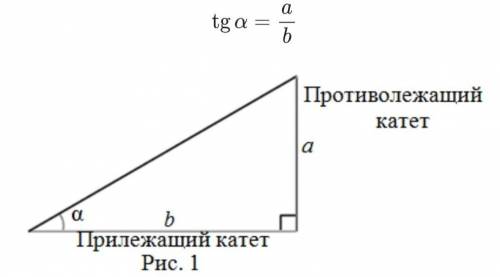
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета (b) к гипотенузе (с) (рис.1)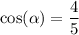
Значит Прилежащий катет b равен 4.
Гипотенуза c равна 5.
a) вычислите tg a
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.По теореме Пифагора найдём противолежащий катет а:
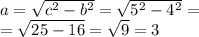
Тогда тангенс α:
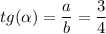
b) используя значение тангенса, постройте угол а
Строим прямоугольный треугольник с противолежащим углу А катетом 3
и прилежащим 4 (рис.2)

Площадь поверхности куба равна 6x².
Отсюда находим сторону куба:
х =√((8а²/6) = √(4а²/3) = 2а / √3.
Диаметр шара, описанного около куба, равен диагонали этого куба.
Диагональ куба равна х√3 = (2а/√3)*√3 = 2а.
Тогда радиус шара равен 2а / 2 = а.