По теореме о трех перпендикулярах отрезок ОВ - проекция наклонной АВ, перпендикулярной прямой ВС (катеты). Следовательно, двугранный угол АВСО измеряется линейным углом АВО по определению и равен 45° (дано). Треугольник АВО прямоугольный и равнобедренный. Катеты АО=ОВ=2см, а гипотенуза АВ=2√2 см. В прямоугольном треугольнике АВС по Пифагору АС=√(АВ² +ВС²) = √(8+4) = 2√3см. В прямоугольном треугольнике АОС синус угла АСО (искомый угол, так как это угол между наклонной АС и плоскостью α по определению) равен отношению АО/АС = 2/(2√3) = √3/3. По таблице - это угол, равный 35,2°.
ответ: 35,2°.
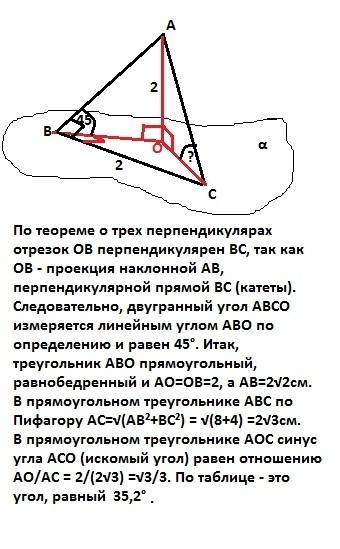
По теореме о трех перпендикулярах отрезок ОВ - проекция наклонной АВ, перпендикулярной прямой ВС (катеты). Следовательно, двугранный угол АВСО измеряется линейным углом АВО по определению и равен 45° (дано). Треугольник АВО прямоугольный и равнобедренный. Катеты АО=ОВ=2см, а гипотенуза АВ=2√2 см. В прямоугольном треугольнике АВС по Пифагору АС=√(АВ² +ВС²) = √(8+4) = 2√3см. В прямоугольном треугольнике АОС синус угла АСО (искомый угол, так как это угол между наклонной АС и плоскостью α по определению) равен отношению АО/АС = 2/(2√3) = √3/3. По таблице - это угол, равный 35,2°.
ответ: 35,2°.

Угол A=30 AD=BC=23 AB=DC=11(По свойствам параллелограмма). Найдём высоту. Проведём высоту BE на сторону AD. Треугольник ABE-прямоугольный. Высота будет равна половине стороне AB=5,5(Катет лежащий против угла в 30 градусов равен половине гипотенузы).Находим площадь по формуле S=a*h. a=AD h=BE S=23*5,5=126,5.