Нужен единичный отрезок. Может быть получен делением отрезка по теореме Фалеса.
1) Гипотенуза треугольника с катетами 1 и 2 равна √5 (по теореме Пифагора)
2) Высота из прямого угла есть среднее пропорциональное проекций катетов на гипотенузу, h=√(AD*DB)
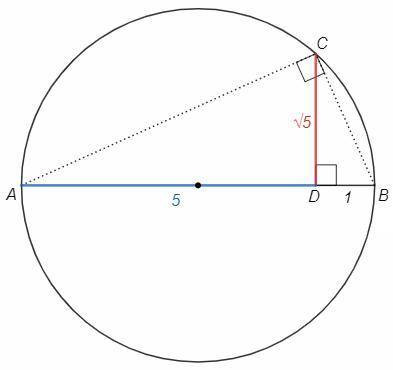
- достраиваем к отрезку AD=5 отрезок DB=1 на одной прямой
- строим окружность на гипотенузе AB
- строим перпендикуляр к AB из точки D
- пересечение перпендикуляра и окружности - C
Вписанный угол ACB - прямой, так как опирается на диаметр. CD - высота из прямого угла.
CD =√(AD*DB) =√(5*1) =√5
сумма внешнего угла треугольника вместе с внутренним равна 180 градусов, поэтому внутренние углы в треугольнике равны 180-107=73градуса, 180-123=57 градусов. Сумма углов в треугольнике равна 180 градусов, поэтому третий угол равен
180-(73+57)=50 градусов. Внешний угол смежный с ним равен 180-50=130 градусов.
сумма внешних углов треугольника, взятых по одному около каждой вершины равна 360 градусов. 123+107+130=360градусов
2)внешний угол равен 88 градусов, значит внутренний угол равен 180-88=92градуса. так как этот угол тупой, то он является вершиной равнобедренного треугольника. Тогда углы при основании равны. По свойству внешнего угла их сумма равна внешнему углу, не смежному с ними, то есть 88 градусов. Каждый угол равен 88:2=44 градуса
Исследуемый четырехугольник - трапеция, подобная данной. Площади подобных фигур относятся друг к другу как квадраты их линейных размеров.
Высота данной трапеции равна sqrt[((24 - 12)/2)^2 + 10^2] = 8.
Площадь данной трапеции равна (12 + 24)*8/2 = 144.
Радиусы вписанных окружностей равны 1, в высоте их вмещается два. Следовательно, высота искомой трапеции равна 8 - 1 - 1 = 6. Высоты этих трапеций относятся как 6/8 = 3/4. Значит, площади трапеций будут относиться друг к другу как 9/16.
И площадь искомого четырехугольника будет равна 144*9/16 = 81.
ответ: 81.
Объяснение: Решение :