если аф равно 1 см, значит FB=1*3=3, тогда AB=1+3=4
AB=BC=4
ответ: 21см²
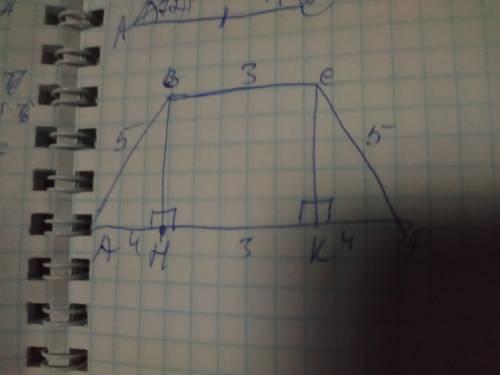
Объяснение: обозначим трапецию АВСД, проведём от двух вершин верхнего основания две высоты и обозначим их ВН и СК. Они делят нижнее основание, так, что в середине нижнего основания получается отрезок равный верхнему основанию трапеции: НК=ВС=3см. Так как трапеция равнобедренная то отрезки АН=КД. Найдём эти отрезки:
АН=КД=(11-3)÷2=8÷2=4см. Рассмотрим полученный ∆АВН. Он прямоугольный где ВН и АН- катеты, а АВ- гипотенуза. Найдём высоту ВН по теореме Пифагора:.ВН²=АВ²-АН²=√(5²-4²)=
=√(25-16)=√9=3. Итак: высота ВН=3см. Площадь трапеции- это полупроизведение его оснований на высоту. Теперь найдём площадь треугольника, зная высоту и основания по формуле: S=(3+11)/2×h=
14/2×3=7×3=21см²
Объяснение:
Известно, что точка пересечения серединных перпендикуляров сторон AB и BC треугольника ABC находится на стороне AC.
1. Докажи, что AD=CD:
Точка D, как точка пересечения серединных перпендикуляров сторон AB и CB, равноудалена от конечных точек этих сторон ( от концов отрезков АВ и СВ) .Если AD =DB и DB = DC следовательно, AD =DC.
2. Определи вид треугольника ADB: -равнобедренный
3. Определи вид треугольника CDB: -равнобедренный
4. Примени соответственное свойство углов и докажи, что∡KBM=∡KAD+∡MCD:
∡ KAD = ∡ KВD, как углы при основании равнобедренного ΔADB ;
∡ MCD = ∡ MВD ,как углы при основании равнобедренного ΔCDB ;
5. Определи вид треугольника ABC: -прямоугольный ,равнобедренный .
Пояснения: Если ∡KAD=х , то ∡MCD=х, ∡KВМ=2х.
По т. о сумме углов треугольника х+2х+х=180° , х=45° ⇒ ∡KAD=45°, ∡MCD=45°, ∡АВС=90°
BF=
1*3= 3 см
АВ=АF+FВ=1+3=4 см
по условию АВ=ВС=4см