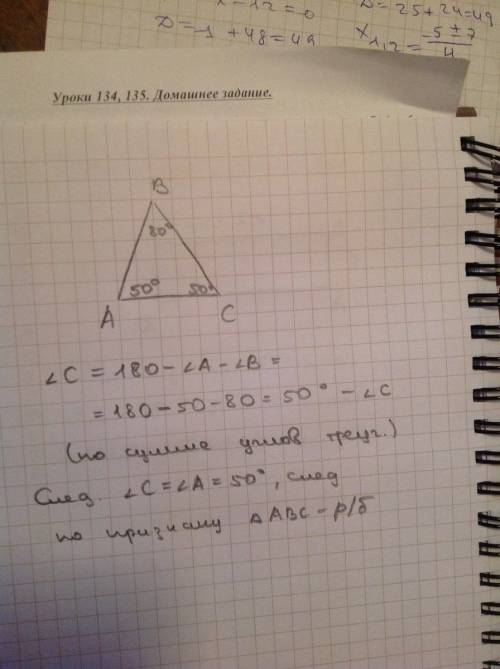
Объяснение:
1. Выполняем построение треугольника АВС.
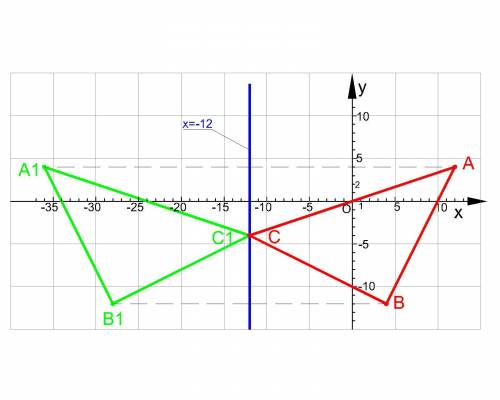
2. Строим график прямой х = -12 . Это вертикальная прямая проходящая через точку (-12; 0)
3. Выполняем построение симметричной фигуры:
от т. А проводим перпендикуляр к прямой х = -12. Откладываем перпендикуляр такой же длины в противоположною сторону от х = -12.
То же самое выполняем для т. В. Т. С совпадает с точкой С1, т.к. абсцисса т. С = -12 и лежит на прямой х = -12.
Координаты ΔA1B1C1 можно определить графически:
А1(-36;4) , В1(-28; -12) , С1(-12; -4).
Также абсциссы можем определить математически:
х1 = -12 - (12+х) = -24-х.
Здесь -12 - это сдвиг координат влево на 12 единиц, (12+х) расстояние между осью симметрии и точками исходного треугольника.
Ординаты остаются неизменными, т.к. ось симметрии - вертикальная.
1)Розглянемо трикутник CPM:<P=90°,<C=20°=> <M=70°.
У трикутнику KPA:<P=90°,<K=70°=> <A=20°.
За теоремою про паралельні прямі <C=<A=20°=>CM||AK.
4)1. Будуємо перпендикуляр;
2. Будуємо кут;
3.Від одного променя кута будуємо гіпотенузу;
4.Візьми кут 45°! Виміряємо кут з верхньої вершини гіпотенузи, також 45°;
5.Будуємо катети.
3) EH—бісектриса, тому <MEH=<AEH=30°. За властивістю катета, який лежить напроти кута 30°:EH=MH*2=6*2=12(см). Розглянемо трикутник EHA: за властивістю рівнобедреного трикутника(кут при основі рівні <AEH=<EAH=30°):EH=AH=12см.
AM=MH+AH=6+12=18(см).
2)<KEM=180°-(<MKE+<KME) ?
не знаю, как-то так