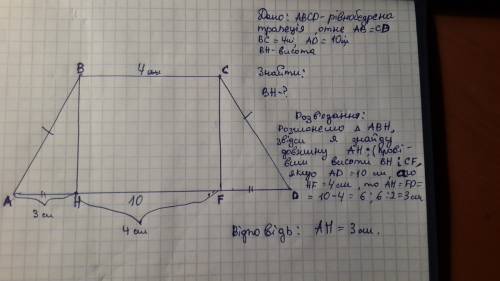
У нас есть 2 варианта внешнего угла — внешний угол угла, противоположному основанию, и внешний угол угла — противоположный боковой стороне.
Вариант 2-ой таков: угол, противоположный боковой стороне равен: 180-150 = 30°, в этом случае — угол, противоположный основанию равен: 180-(30+30) = 120°.
Боковая сторона равна 10, тоесть нам уже известно 2 стороны равнобедренного треугольника (боковые).
Теперь — зная их, и угол между ними (угол 120 градусов) — найдём основание по теореме Косинусов:
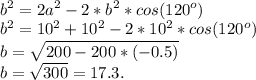
Нам известны все стороны равнобедренного треугольника.
Формула вычисления радиуса описанной окружности около равнобедренного треугольника такова:
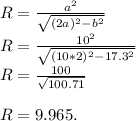
Диаметр в 2 раза больше радиуса, то есть: D = 2R = 19.93.
Вывод: D = 19.93.
Вариант 1-ый:
Внешний угол угла — противоположного основанию, тоесть: α = 180-150 = 30°.
Равные углы, противоположные боковым сторонам равняются: (180-30)/2 = 75°.
На этот раз — формула вычисления основания, зная боковую сторону, и угол между ними — будет такова:

В этом случае — радиус описанной окружности равен:
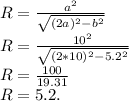
D = 2R = 5.2*2 = 10.4.
Вывод: D = 10.4.
Доказано // Удачи ;D
Объяснение:
Сделаем это задание за Теоремой про равность треугольников
Мы знаем что ab = ad тогда треугольник abd - равнобедренный треугольник и также треугольник bdc равнобедренный треугольник
Тогда за третей ознакой равенства:
1. AB = AD
2. BC = CD
3. сторона AC - общая.
Значит, ∠BAO = ∠DAO
Тогда За 1 признаку докажем что эти треугольники равны, так как мы нашли что углы равны
( Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. )
AB = AD AO - общая
∠BAO = ∠DAO за 3 ознакой. С этого ΔABO = ΔADO
Из равенства ΔABO и ΔADO вытекает равенство углов ∠BOA и ∠DOA. поэтому ∠BOA = ∠DOA = 90°. Следовательно AC⊥BD
И этим мы доказали что O - середина BD
Доказано // Удачи ;D