Нехай маємо прямокутний трикутник ABC (∠C=90), у якого AC=√5 см – катет і BH=4 см – проекція катета BC на гіпотенузу AB (за умовою).
прямокутний трикутник, рисунок Проведемо висоту CH=h до гіпотенузи AB (AB⊥CH).
За властивістю прямокутного трикутника
h^2= AH•BH
(це виводиться із подібності прямокутних трикутників ABC і CBH).
Нехай AH=x - проекція катета AC на гіпотенузу AB, тоді h^2=4x.
У прямокутному ΔACH (∠AHC=90), у якого AH=x і CH=h=2√x – катети, AC=√5 см – гіпотенуза, за теоремою Піфагора запишемо:
AH^2+CH^2=AC^2, x^2+4x=5, x^2+4x-5=0,
за теоремою Вієта, отримаємо
x1=1 і x2=-5<0, звідси AH=1 см.
AB=AH+BH=1+4=5 см – гіпотенуза ΔABC.
Відповідь: 5.
Объяснение:
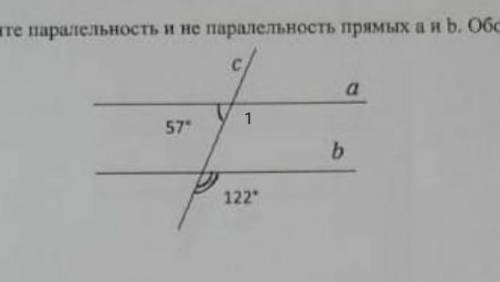
1)
Прямая, это развернутый угол.
<1=180°-57°=123° (<1- отметила на чертеже)
Так как <1≠<122°, то прямые а∦b, так как соответственные углы не равны.
ответ: а∦b.
3)
Если два внешних угла равны, то и два внутренних угла равны.
Отсюда следует, что треугольник равнобедренный (углы при основании равны)
1) решение
Пусть основание треугольника будет равно 25, найдем боковые стороны.
(83-25)/2=29см.
ответ: стороны треугольника равны 25см; 29см; 29см
2) Решение
Пусть боковая сторона треугольника будет 25, найдем основание.
83-25*2=83-50=33см.
ответ: стороны треугольника равны: 25см; 25см; 33см.
4)
<САВ=180°-120°=60°. (Внутренний угол <А треугольника).
Так как треугольник прямоугольный
То <В=90°-<А=30° (Сумма острых углов в прямоугольном треугольнике равна 90°)
СА - катет который лежит против угла 30°. Равен половине гипотенузы (СА=1/2*АВ).
Пусть СА будет х; тогда АВ будет 2х.
Составляем уравнение.
х+2х=33
3х=33
х=33/3
х=11 см сторона СА.
11*2=22 см сторона АВ
ответ: СА=11см; АВ=22см