ответ: V=64√5см³
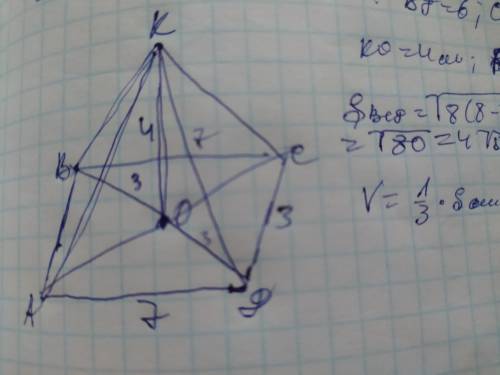
Объяснение: обозначим вершины пирамиды АВСД с высотой КО и диагоналями ВД и АС. Одна диагональ делит параллелограмм на 2 равных треугольника. Пусть ВД=6см. Рассмотрим полученный ∆ВСД. В нём известны 3 стороны и мы можем найти его площадь по формуле: S=√((p-a)(p-b)(p-c)), где а сторона треугольника а р-полупериметр:
Р=3+7+6=16см; р/2=16/2=8см
S=√8((8-7)(8-6)(8-3))=√(8×1×2×5)=
=√80=8√5см²
Так как таких треугольников 2, то площадь параллелограмма=8√5×2=16√5см²
Теперь найдём объем пирамиды зная площадь основания и высоту по формуле: V=⅓×Sосн×КО=
=⅓×16√5×4=64√5/3см³
Площадь квадрата равна его стороне в квадрате. Из условия мы можем найти стороны этих двух квадратов. Все стороны квадрата равны а так как каждый из этих квадратов построен на одной из стороне прямоугольника, то следовательно сторона квадрата равна стороне прямоугольника. Извлекаем квадратный корень из площадей квадрата и получаем стороны прямоугольника: 7 см и 12 см.
Периметр прямоугольника равен удвоенному произведению суммы его сторон:
2*(7 + 12) = 38 см - периметр вашего прямоугольника.
ответ: перемитр прямоугольника равен 38 см.