ответ: S=π•[(ab/(a+b)]²
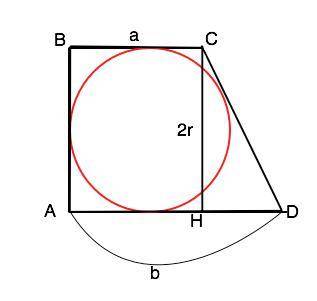
Объяснение: Обозначим трапецию АВСD, ВС||AD, СВА=ВАD=90°. ВС=а, AD=b.
Формула площади трапеции
Ѕ=0,5•(а+b)•h
Высота трапеции равна диаметру вписанной окружности=2r ⇒
S=(a+b)•2r/2 ⇒
r=S/(a+b)
Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. S=ab
ab=(a+b)•r ⇒ r=ab/(a+b)
S(круга)=πr²
S=π•[(ab/(a+b)]²
* * *
Несложно доказать, что в такой трапеции S=ab, если соединить вершины С и D с центром окружности и выразить r=высоту прямоугольного ∆ СОD из произведения отрезков касательных, но это уже другая задача.
* * *
Задачу можно решить и другим
Если в четырехугольник вписана окружность. суммы длин его противоположных сторон равны.
Тогда АВ+CD=a+b. В прямоугольном треугольнике СНD по т.Пифагора СН²=СD²-DH²
CH=2r, HD=AD-BC=b-a, а CD=a+b-2r. Найденный радиус также будет ав/(а+в)
ответ: S=π•[(ab/(a+b)]²
Объяснение: Обозначим трапецию АВСD, ВС||AD, СВА=ВАD=90°. ВС=а, AD=b.
Формула площади трапеции
Ѕ=0,5•(а+b)•h
Высота трапеции равна диаметру вписанной окружности=2r ⇒
S=(a+b)•2r/2 ⇒
r=S/(a+b)
Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. S=ab
ab=(a+b)•r ⇒ r=ab/(a+b)
S(круга)=πr²
S=π•[(ab/(a+b)]²
* * *
Несложно доказать, что в такой трапеции S=ab, если соединить вершины С и D с центром окружности и выразить r=высоту прямоугольного ∆ СОD из произведения отрезков касательных, но это уже другая задача.
* * *
Задачу можно решить и другим
Если в четырехугольник вписана окружность. суммы длин его противоположных сторон равны.
Тогда АВ+CD=a+b. В прямоугольном треугольнике СНD по т.Пифагора СН²=СD²-DH²
CH=2r, HD=AD-BC=b-a, а CD=a+b-2r. Найденный радиус также будет ав/(а+в)

S(боковой поверхности)=а²·6=294
а=7
высота=7
2)АС=4
BD=3
AO=AC/2=2
OD=BD/2=1,5
по теореме Пифагора
AD²=AO²+OD²=4+2,25
AD=2,5
CC1²=DC1²-DC²=42,25-6,25
CC1=6
S(полной поверхности)=2S(ABCD)+4S(AA1D1D)=2·3·2+4·2,5·6=12+60=72
3)EH=AD/2
ES=EH/cos60=2/(1/2)=4
S(полной поверхности)=S(ABCD)+4S(ABS)=16+8·4=48