Что и требовалось доказать!
Объяснение:Перпендикулярные прямые - прямые, которые пересекаются и при пересечении образуют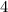 
прямых угла. (углы, градусная мера которых составляет 
).
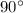Допустим, данные прямые перпендикулярны.
Тогда все три угла равны по .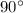
Сумма градусных мер трех неразвернутых углов, образованных при пересечение двух прямых, меньше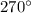 
, по условию.
Проверим: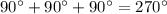 
Исходя из этого, мы доказали, что прямые не перендикулярны, так как сумма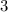 
неразвёрнутых углов составляет ровно 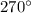, что не соответствует условию.
Что и требовалось доказать!
Объяснение:Перпендикулярные прямые - прямые, которые пересекаются и при пересечении образуют 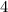прямых угла. (углы, градусная мера которых составляет ).
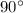Допустим, данные прямые перпендикулярны.
Тогда все три угла равны по .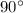
Сумма градусных мер трех неразвернутых углов, образованных при пересечение двух прямых, меньше 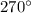, по условию.
Проверим: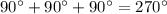
Исходя из этого, мы доказали, что прямые не перендикулярны, так как сумма 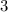неразвёрнутых углов составляет ровно 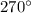, что не соответствует условию.
<BCD=65
<ABC=<ADC=35 так как опираются на одну и ту же дугу AC
тогда из треугольника ABC:
найдем <BAC= 180-(<BAC+<BCA)=180-(65+35)=80
ответ: 80
№ 2 AO - радиус окружности, перпендикулярный касательной AD
AO=OB=R
<BAD=160
O - центр окружности
так как радиус перпендикулярен касательной, то <OAD=90, тогда <OAB=160-90=70
AO=OB, значит треугольник AOB - равнобедренный, то <BAO=<ABO=70
<BOA=180-(70+70)=40
ответ: 70, 70, 40