ΔKLM — прямоугольный, ∠L = 90°.
∠K = 90°−∠M = 90−45 = 45° ⇒ ΔKLM — равнобедренный: ML = KL
Биссектриса, проведенная к основе равнобедренного треугольника является медианой и высотой. Медиана, проведенная из прямого угла тр-ка, равна половине гипотенузы:
LN = MN = KN = 16/2 = 8 (cm)
Отрезок NS — расстояние от точки N до стороны LM, (NS⊥ML).
Из прямоугольного треугольника MSN: ∠SNM = 90°−∠NMS = 90−45 = 45° ⇒ ΔMSN — равнобедренный: MS = NS:
MS = NS = x, тогда из т. Пифагора:
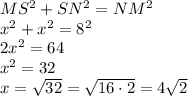
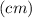
MS = NS = x = 4√2 ≈ 5,65 (cm)
5 < NS < 6
∠NLM = ∠NLK = 90/2 = 45° (т.к. LN — биссектриса) ⇒ Δ NML и ΔNLK — равнобедренные. Отрезки NS NR — высоты, биссектрисы и медианы Δ NML и ΔNLK соответственно ⇒
⇒ MS = LS = NS = 4√2 (cm) и KR = LR = NR = 4√2 (cm);
Следовательно, отрезок RS — средняя линия ΔKLM:
Средняя линия тр-ка равна половите стороны, к которой она параллельна: RS = KM/2 = 16/2 = 8 (cm).
расстояние от точки N до стороны LM заключено между целыми числами 5 и 6;длина отрезка RS равна 8 cm.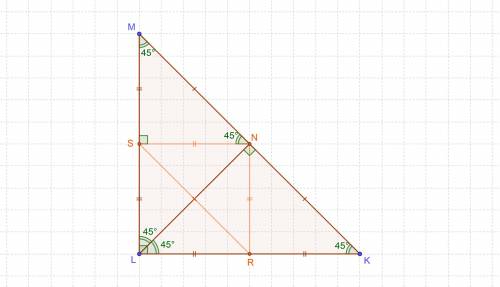
Объяснение:
Назовём вершины треугольника
Найдем гипотенузу:
по теореме Пифагора:
АВ²=АС²+ВС²
подставим значения:
АВ²=2²+(2√3)²
АВ²=4+12
АВ²=16
АВ=4
значит длина гипотенузы АВ равна 4.
По теореме: если в прямоугольном треугольнике один из катетов меньше гипотенузы вдвое, то данный катет лежит против угла в 30°.
АС=2;
АВ=4
4÷2=2
Следовательно катет АС вдвое меньше гипотенузы АВ, исходя из этого угол АВС=30°
В прямоугольном треугольнике сумма острых углов 90°.
Найдём угол ВАС
ВАС=90°–угол АВС=90°–30°=60°
ответ: угол ВАС=60°; угол АВС=30°
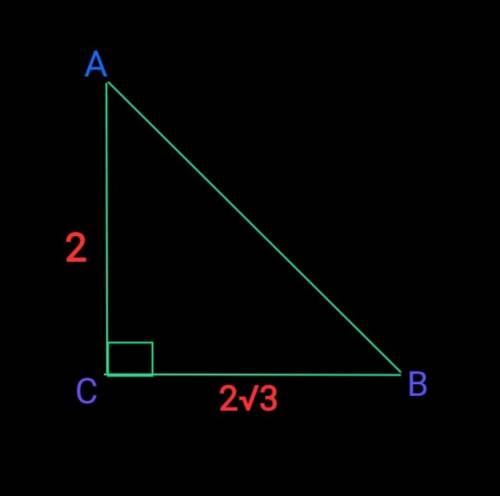
R=a/√3=√3/√3=1
L=2πR=2π≈2*3,14=6,28