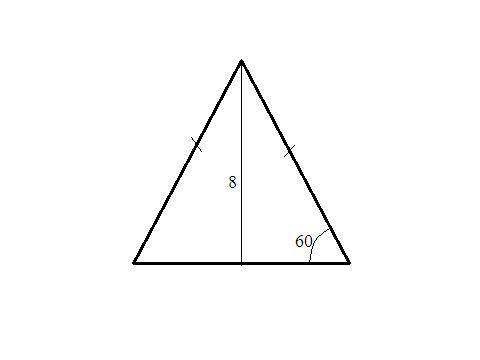
Объяснение:
Осевое сечение конуса - равнобедренный треугольник с боковыми сторонами (образующие конуса), основание - диаметр основания.
Треугольник, образованный высотой, образующей и половиной диаметра - прямоугольный. Угол при вершине (90-60)=30° ⇒ половина диаметра (катет против угла 30°) равен половине образующей (гипотенуза). По т. Пифагора -
(2х)²=8²+х²
х²=8²/3
х=8/√3;
Площадь - S=a*h/2, где а=2х=16/√3, h=8;
S=16*8/(2√3)=64/√3=64√3/3.
Можно проще.
Угол при основании 60° ⇒ треугольник равносторонний.
S=h²/√3=8²/√3=64/√3=64√3/3.
1) 150.
2) 15.
3) 18.
4) 270.
Объяснение:
Площадь трапеции определяется по формуле:
S=h(a+b)/2;
1) a=9+12=21; b=4; h=12.
S=12*(21+4)/2=6*25=150;
***
2) S=h(a+b)/2; a=3; b=9; h=? Высота (катет )лежит против угла в 30* и равна половине гипотенузы h=5/2=2.5;
S=2.5(3+9)/2;
S=2.5*12/2;
S=2.5*6=15.
***
3) Вероятно это равнобокая трапеция и углы при основаниях равны.
Проведем высоту из вершины тупого угла. Получим равнобедренный треугольник с углами по 45*, стороны которых (и высота) равны 9-2*3=9-6=3;
S=h(a+b)/2; h=3; a=3; b=9;
S=3(3+9)/2=3*12/2=18.
***
4) Все величины для нахождения площади известны.
S=h(a+b)/2; h=15; a=4; b=8+24=32;
S=15(4+32)/2;
S=15*36*2=15*18=270.
1) Любые три различные прямые проходят через одну общую точку.
Неверно
А если прямые параллельны?
Две прямые в пространстве либо пересекаются (имеют одну общую точку), либо скрещиваются, либо параллельны
2) Существует точка плоскости, не лежащая на данной прямой, через которую нельзя провести на плоскости ни одной прямой, параллельной данной.
Неверно.
Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной. ( И почему бы этой точке не лежать на плоскости?)
3) Если угол равен 47°. то смежный с ним угол равен 47°.
Неверно. Смежный угол равен 180-47=133°
4) Через любые две различные точки плоскости можно провести прямую.
Верно. Это аксиома, доказательств не требует и звучит так:
Через любые две точки можно провести прямую, и только одну.
5) Существуют две различные прямые, не проходящие через одну общую точку.
Верно. Эти прямые - параллельные на одной плоскости или расположены в параллельных плоскостях.