Отрезок АВ делим в на 4 (т.к. у нас всего 4 части 1+3) и находим координату точки С = 48 (можно представить что отрезок АВ совмещен с осью ОХ например и точка А совпадает с О а точка В имеет координату 192). Середина отрезка СВ будет иметь координату (192-48)/2 + 48 = 120 длина СВ =192-48=144 обозначим её например Х1 теперь найдем координату точки D для этого посчитаем 1/12 от СВ = 12 и отложим влево от точки С т.е. 48-12=36 середина отрезка АD иметь координату 36/2=18 её можно обозначить Х2 теперь чтобы узнать длину отрезка Х1Х2 нужно из координат точки Х1 вычесть координаты точки Х2 т.е. 144-18=126 (дм)
Так же, как прямую определяют 2 точки, так и плоскость определяют три точки. То есть через любые три точки пространства можно провести плоскость и притом только одну. Беря поочередно по три точки из четырех имеющихся так, чтобы одна точка все время находилась вне той плоскости, которую мы в данный момент строим, получаем 4 различные плоскости, каждая из которых включает в себя три точки из имеющихся четырех. Единственное условие: эти 4 точки не должны лежать в одной плоскости...)) Иначе плоскость получится только одна...)))
В прямоугольном ΔBAD (∠A=90°):
AB=4·3см, BD=4·5см значит, по Египетскому треугольнику AD=4·4см=16см.
AD = BC = 16см, как противоположные стороны прямоугольника ABCD.
В прямоугольном ΔABM (∠B=90°):
AB=12см, AM=13см значит, по Пифагоровой тройке BM=5см;
Ну или по теореме Пифагора BM = √(AM²-AB²) = √(13²-12²) = √((13-12)(13+12)) = √25 = 5 см.
MC = BC-BM = 16-5 = 11 см
S(AMCD) = S(ABCD) - S(ABM) = AB·AD - AB·BM = 12·16-12·5:2 = 6·(32-5) = 6·27 = 162 см²
AB·BM = 12·16-12·5:2 = 6·(32-5) = 6·27 = 162 см²
ответ: MC=11см и S(AMCD)=162см².
Можно было найти S(AMCD), как площадь трапеции, основания которой MC=11см, AD=16см и высота CD=AB=12см. Тогда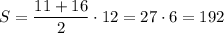 см².
см².