1) Треугольник ОСВ равнобедренный, т.к. ОС = ОВ как радиусы одной окружности. Следовательно, углы ОСВ и ОВС при основании этого треугольника равны. Т.к. сумма углов треугольника равна 1800, то OCB = OBC = (1800 - COB) : 2 = (1800 - 490) : 2 = 65,50.
2) Аналогично: треугольник ОАВ равнобедренный, т.к. ОА = ОВ как радиусы одной окружности. Следовательно, углы ОАВ и ОВА при основании этого треугольника равны. Т.к. сумма углов треугольника равна 1800, то OАB = OBА = (1800 - АOB) : 2 = (1800 - 950) : 2 = 42,50.
3) Искомый угол В, он же угол АВС, равен 65,50 + 42,50 = 1080.
ответ: 108
P.S. В задаче лишние данные: как видим, углы, которые стягивают дуги CD и AD, и которые равны и, здесь абсолютн
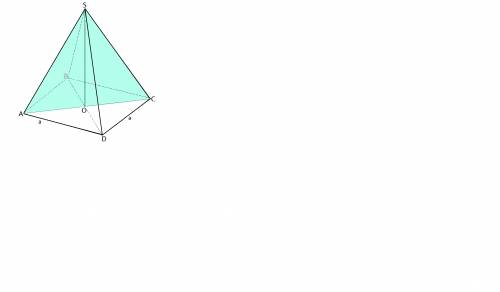
Cторона основания правильной четырехугольной пирамиды равна а, а ее диагональное сечение - равносторонний треугольник.
Найдите обьем пирамиды
Объём пирамиды равен одной трети произведения площади основания на ее высоту.
Площадь основания - площадь квадрата-
S ABCD=а²
Высоту найдем исходя из того, что диагональное сечение пирамиды - правильный треугольник АSС.
Стороной этого треугольника является диагональ АС основания.
Диагональ квадрата равна а√2
АС=АS=SC=а√2
Так как углы правильного трегуольника равны 60°, высота пирамиды
SO=АS·sin(60°)=(а√2·√3):2=а√6):2
Объем пирамиды
V={(а²·а√6):2}:3=(а³√6):6
В точке x0=1 значение производной равно: 8*1^3-4=4
Значит уравнение касательной будет следующим: у=4x+c. Чтобы найти c, надо узнать значение самой функции в точке x0=1. Считаем:
2*1^4-4*1 =2-4=-2
И подставляем в уравнение: -2=4*x0+c; -2=4+с; с=-4-2; с=-6.
Окончательно получаем уравнение нашей касательной y=4x-6
Вроде так как-то.