Можно решить
Из прямоуг. треуг-ка АОВ найдем катеты( равны радиусу) 2Rквад = 324, или Rквад = 162. Теперь по известной формуле для прямоуг. тр-ка найдем искомое расстояние, а именно - высоту, опущенную на гипотенузу:
h = Rквад/АВ = 9см
треугольник АОВ - равнобедренный и прямоугольный по теореме Пифагора ОА = ОВ = 18 : sqrt2 = 9*sqrt2 обозначим h - расстояние от точки О до хорды, этот отрезок будет перпендикулярен хорде тогда площадь треугольника АОВ = ОА*ОВ/2 = АВ*h/2 отсюда h = ОА*ОВ/АВ = (9*SQRT2)^2/18 = 9 см
1.наибольший угол лежит ПРОТИВ наибольшей стороны АС=10см, и это угол В=90°, просто треугольник избитый, египетский.)
2. Значит, второй равен 60°, т.к. сумма острых угло в прямоугольном треугольнике равна 90°.
3. Значит третий равен 180°-100°=80°, т.к. сумма всех углов в треугольнике равна 180°.
4. Еще как существует!) он является прямоугольным, т.к. 3²+4²=5²
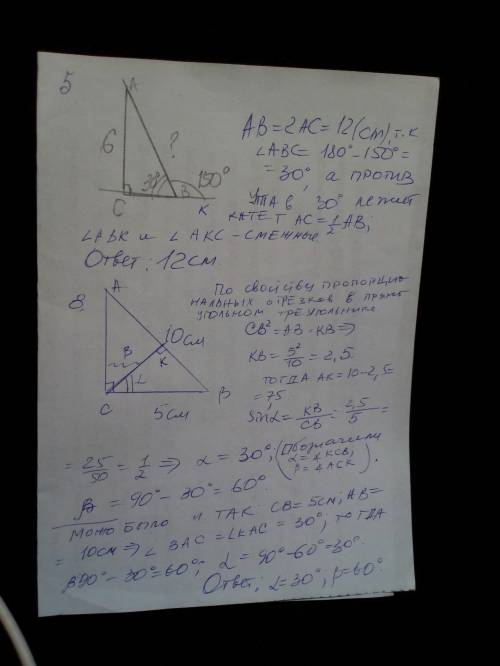
5. во вложении
6. пусть х- коэффициент пропорциональности, тогда 3х+х+2х=180, х=30, меньший угол 30°, второй угол 2*30°=60°, и третий 3 *30°=90°
8. во вложении
а)2√3
б)3√5
Найдите радиус шара.
Всякое сечение шара плоскостью - круг. Плоскость треугольника пересекается с шаром по окружности, вписанной в данный треугольник. Точки касание сторон и шара - точки касания вписанной в треугольник окружности.
Чтобы найти радиус шара, нужно найти длину отрезка, соединяющего его центр с точкой касания со стороной треугольника.
Пусть радиус шара ОС будет R, радиус О₁С вписанной в треугольник окружности - r , расстояние от центра шара до плоскости треугольника ОО₁- а.Тогда по т.Пифагора
R=√(a²+r²)
Радиус вписанной в треугольник окружности найдем по формуле
r=S/p, где S - площадь треугольника, р- его полупериметр.
p=(7+15+20):2=21
По формуле Герона площадь треугольника
S=√21*(21-20)*(21-15)*(21-7)=√(21*1*6*14)=√(3*7*2*3*2*7)=2*3*7=42
r=42/21=2
a) OO₁=2√3
R=√((2√3)²+2²)=√16=4 cм
б) ОО₁=3√5
R=√((3√5)²+2²)=√49=7 см