Объяснение:
При длине рейки в 3 см достичь точки (4,5) невозможно, поскольку расстояние от начала первой рейки до конца второй (в случае, если обе рейки лежат на одной прямой) составляет 3 + 3 = 6 см, а кратчайшее расстояние до точки (4,5) составляет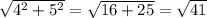 
, что больше 6.
Допустим, нужная нам точка имеет координаты (x,y), а длина рейки равна S. Тогда кратчайшее расстояние до точки равно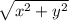 
, и 2 рейки в сочетании с этим расстоянием составляют равнобедренный треугольник со сторонами S, S и .
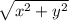По теореме косинусов в треугольнике со сторонами a, b и c и углом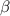 
справедливо соотношение 
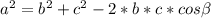. Для нашего треугольника данное выражение примет вид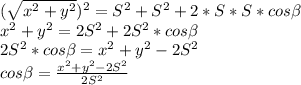 
Отсюда искомый угол будет равен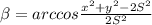 
.
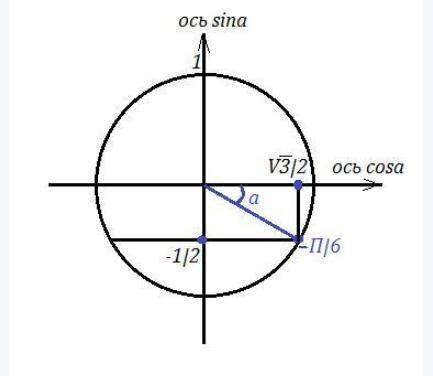
1. а)Уравнение окружности х²+у²=1 этой окружности принадлежит точка В(√3/2;-1/2), т.к. подставляя в уравнение окружности, получим
3/4+1/4=1. остальные не подходят.
б) Эта точка лежит в четвертой четверти, ей соответствует угол 330°, или в радианной мере 11π/6; косинус этого угла равен абсциссе точки, т.е. √3/2, синус - ее ординате, т.е. -1/2, тангенс - отношение синуса к косинусу, т.е. -1/√3=-√3/3, а котангенс обратен тангенсу, и равен -√3. Проверим, например синус sin330°=sin(360°-30°)=sin30°=-1/2
cos330°=cos(360°-30°)=cos(-30°)=cos30°=√3/2
2. по теореме косинусов х²=а²+b²-2ab*cosα; третья сторона х=√(25+16-2*4*5*0.5)=√21/см/; периметр равен 4+5+√21=(9+√21)/см/
Площадь найдем по формуле s=(a*b*sinα)/2=(4*5*sin60°)/2=20√3/см²/
Радиус окружности, описанной около этого треугольника найдем по следствию из теоремы синусов. а/sinα=2R⇒R=a/(2sinα)=
√21/(2√3/2)=√7/cм/
3. по теореме синусов 12/sin50°=32/sinα⇒sinα=32*sin50°/12=
32*0.766/12≈2/043, решений ноль, т.к. не может синус угла быть больше единицы.
Вне шара дана точка А на расстоянии 10 см от его поверхности.
Найти
длину такой окружности на поверхности шара, все точки которой отстают от А на 20 см Расстояние измеряется перпендикуляром. А находится на отрезке прямой, перпендикулярной диаметру искомой окружности. Точка А от центра шара удалена на 15+10=25 см ( радиус + расстояние)
Все точки искомой окружности находятся на поверхности окружности основания воображаемого конуса, "надетого" на шар.
Смотрим схематический рисунок - разрез шара через центр и точку А.
АО=15+10=25 см.
ОК=R
АК - расстояние, на которое должна быть удалена точка А от поверхности.
КМ- диаметр искомой окружности,КН - ее радиус.
Имеем треугольник АКО со сторонами, отношение которых 3:4:5 - отношение прямоугольного "египетского" треугольника.
Радиус искомой окружности КН - высота этого треугольика.
Чтобы найти высоту, применим свойство катета прямоугольного треугольника:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
Пусть отрезок гипотенузы, заключенный между катетом и высотой,
ОН =х
Тогда
ОК ²=х*25
25х=225
х=9
Из треугольника КНО
КН²=КО²-ОН²= 225-81=144
КН=r=12 см
Длина окружности с радиусом 12 см
С=2πr= 2π12=24π cм