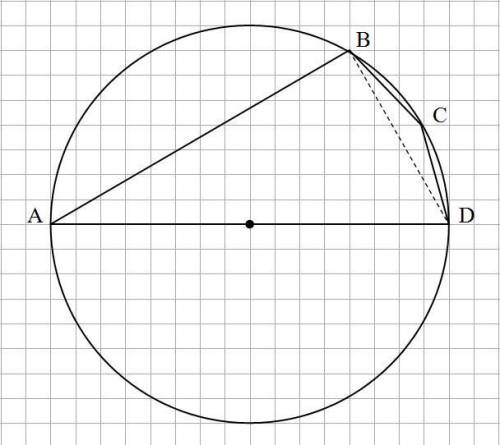
См. рис.
Так как AD - диаметр окружности, то угол ∠ABD = 90°
Следовательно, оставшийся угол прямоугольного
треугольника ΔABD: ∠BAD = 90 - 65 = 25°
Так как угол ∠BAD - вписанный, то величина дуги, на которую он опирается:
∪BCD = 2 · ∠BAD = 50°
Искомый угол ∠С = ∠BCD опирается на оставшуюся дугу
окружности:
∪BAD = 360 - ∪BCD = 360 - 50 = 310°
И величина угла ∠С = 310 : 2 = 155°
Причем, величина угла ∠С не зависит от местоположения точки С на дуге ∪BCD, так как в любом случае этот угол опирается на дугу ∪BAD, равную 310°
-b(-2;0;1)
2a-b(4;-2;-7)
2)1/2a(1;0;-2)
-b(2;-3;1)
1/2a-b(3;-3;-1)
|1/2a-b|=√(9+9+1)=√19