Объяснение:
Дано:
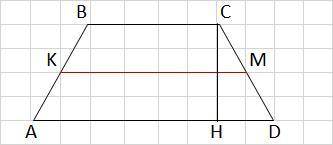
ABCD - трапеция
АВ = CD
ВС = 4
СН - высота
КМ = 10 (средняя линия: АК = КB, СМ = MD)
HD = ?
1) АВ = CD, т.е. трапеция - равнобедренная
2) Свойство трапеции: средняя линия трапеции параллельна основаниям и равна полусумме оснований:
КМ = (ВС + AD)/2
10 = (4 +AD)/2 → 20 = 4 + AD → AD = 20 -4 → AD = 16
3) Свойство равнобедренной трапеции:
Высота (CH), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AH), который равен полусумме оснований и меньший (HD), равный полуразности оснований:
HD = (AD - BC)/2 = (16 - 4)/2 = 6
HD = 6.
Если это треугольник, то тут и решать нечего, поскольку центр обеих окружностей совпадает с точкой пересечения медиан, а сама медиана как раз и делится этим самым центром на 2 отрезка, один из которых радиус описанной, а другой - вписаной окружности. Поэтому медиана (высота, биссектриса) равна сумме радиусов, то есть сумме длин окружностей, деленной на 2 пи.
(7*корень(3)*пи)/(2*пи) = 7*корень(3)/2;
сторона поэтому равна 7 (поделил на синус 60 градусов), а периметр 21.
Если же многоугольник произвольный, то тут решение зависит от числа сторон. Уточните.