1. Построение чертежа.
ВС и АD - столбы; АВ - расстояние между столбами; СD - перекладина.
Переворачиваем чертёж, получаем прямоугольную трапецию АВСD.
2. Решение задачи (х-неизвестное на чертеже).
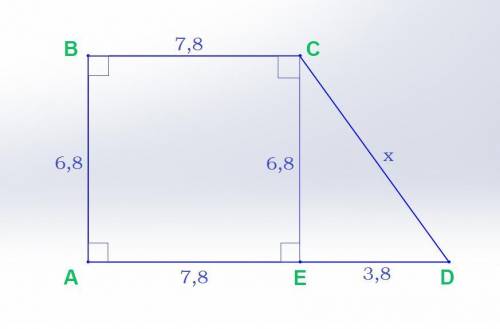
1) Провели высоту СЕ трапеции АВСD.
Получили прямоугольник АВСЕ, в котором ВС=АЕ, СЕ=АВ (по св-ву прямоугольника). Следовательно, высота СЕ=6,8м.
2) Если АЕ=ВС=7,8м, а АD=АЕ+ЕD, то ЕD=11,6м-7,8м=3,8м.
3) Рассмотрим ΔСЕD (прямоугольный). В нём известны 2 катета.
По т.Пифагора найдём гипотенузу СD.
СD²=СЕ²+ЕD² ⇔ СD=√6,8²+3,8² ⇔ СD=√60,68м.
3. ответ: длина перекладины √60,68м.
p.s. если нужно приблизительное рациональное число, то длина перекладины 7м<CD<8м или ≈7,79м.
ответ: 1650 м² и 3600 м²
Объяснение:
1)S=a*b; сторона b=a+20
По т.Пифагора d²=a²+b²
a²+(a+20)²=(10√37)²
a²+a²+2*a*20+20²=100*37
2a²+40a-3300=0
a²+20a²-1650=0
D=20²-4*1*(-1650)=7000
a=(-20+√7000)/2=5√70-10 м
b=a+20=5√70-10+20=5√70+10 м
S=a*b=(5√70-10)(5√70+10)=25*70-100=1650 м² - площадь участка 1 соседа
2)Р=2*(a+b)=240; тогда a+b=120, выразим а= 120-b
Половина диагонали равна 30√2, значит вся диагональ 60√2
По т.Пифагора d²=a²+b²и подставим а= 120-b
(120-b)²+b²=(60√2)²
14400-2*120*b+b²+b²-3600*2=0
2b²-240b+7200=0
b²-120b+3600=0
По т.Виета b=60 м
тогда а= 120-b=120-60=60 м
S=a*b= 60*60=3600 м² площадь участка 2 соседа
S(диагонального сечения)=1,414*4*4=22,6
Должно быть как-то так