Задача решена Пользователем Рисадес Хорошист
Исправлена неточность в последнем действии.
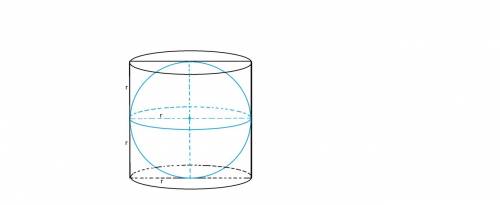
Шар может быть вписан в цилиндр только тогда, когда этот цилиндр правильный, т.е. когда его осевое сечение является квадратом.
Радиус основания цилиндра равен радиусу шара и равен r.
Высота цилиндра равна диаметру основания и равна 2 r.
Полная площадь поверхности складывается из площади двух оснований и площади боковой поверхности:
2*πr² + 2πr*2r = 6πr²
Площадь шара = 4πr²
Площадь цилиндра больше площади шара в
6πr² : 4πr² = 1,5 (раза)
Площадь полной поверхности шара
111 : 1,5 = 74 ( единиц площади)
тр. KMP прямоугольный т.к. MB высота
угол MKP = 45 по условию, по свойству суммы углов тр-ка угол KMB = 45 ⇒ тр. KMB равноберенный прямоугольный. KB=MB=6 см
S=1/2bh
S=1/2*(6+8)*6=1/2*14*6=42 см²