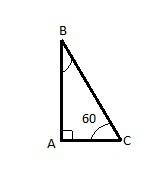
Построим прямоугольный треугольник АВС (угол А= 90 градусов, угол С=60 градусов).
Сумма углов треугольника равна 180 градусам. Зная это найдем угол В:
В=180-(А+С)=180-(90+60)=30 градусов.
Так как против меньшей стороны треугольника лежит меньший угол то меньшим катетом треугольника АВС будет сторона АС (В<С<А)
Катет, лежащий против угла 30 градусов равен половине гипотенузы.
Пусть катет АС=х см. Тогда гипотенуза ВС=2х см. Получаем уравнение:
х+2х=21
3х=21
х=21/3
х=7
Катет АС=7 см.
Гипотенуза ВС=2*7=14 см.
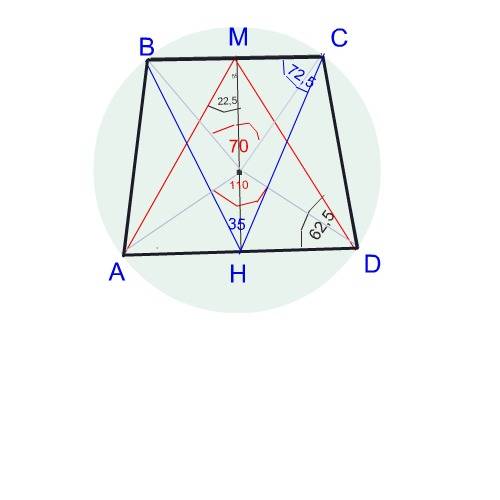
Рисуем трапецию в окружности.
Дополним рисунок треугольниками АМD и ВНС.
Углы при вершинах этих треугольников равны половине центральных углов ( под которыми видны из центра окружности основания трапеции)
Путем несложных вычислений находим углы треугольников DМН и МНС
Для решения применена теорема синусов.
Синусы найденных углов
72,5=0,9537
62,5=0,8870
22,5=0,3826
17,5=0.3007
---------------------------------
МН:sin 62,5=8:0,887=9,019
DН=9,019∙ sin22,5=3,4507
AD=6,9
-------
МН:sin 72,5=8:0,9537=8,3884
СМ=8,3884∙sin17,5=2,52
ВС=5,04
Ясно, что значения длин сторон округленные.
-------------
Площадь трапеции равна произведению полусуммы оснований на ее высоту.
S ABCD=8(6,9+5,04):2=95,52 (?)³
По свойству параллелограмма DA=СВBM:MC=2:3, значит, СМ=3*СВ/5=3*DA/5=3*а/5СА=DA-DC=а-bMA=CA-CM=3*a/5-(a-b)=b-2*a/5
ответ:b-2*a/5