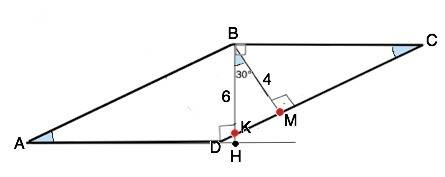
ВМ ⊥ CD, но ВН не является гипотенузой прямоугольного треугольника, образованного высотами, т.к. ВМ:ВН =4/6, и это отношение не равно cos30°
ВН пересекает СD в т.К.
∆ ВКМ - прямоугольный, угол МВК=30°, след, угол ВКМ=60°. Тогда в подобном ему по общему острому углу при К прямоугольном ∆ ВКС
угол ВСК=30°
Катет ВМ противолежит углу 30°, след. гипотенуза ВС=2 ВМ=8 см.
В параллелограмме противоположные углы равны.
След. ∠ВАН=BAD=30°, и катет ВН противолежит углу 30°, ⇒ гипотенуза АВ=2 ВН=12 см.
Площадь параллелограмма равна произведению высоты на сторону, к которой проведена.
CD=AB=12 см
S= CM•CD=4•12=48 см²
* * *
Или
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними:
S=a•b•sinα
S=12•6•sin30°=96•1/2=48 см
Т.к призма правильная, то в основании всегда лежит квадрат, отсюда площадь основания равна: 25. Но оснований два у нас и оба они равны, тогда площадь обоих оснований равна: 25*2=50
Имеем четыре равных прямоугольника - боковые грани призмы. Площадь одного прямоугольника: 5*8=40. Отсюда площадь 4 прямоугольников: 4*40=160 - одновременно площадь боковой поверхности.
Площадь полной поверхности: 50+160=210