меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
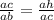
теперь подставим наши значения в эту пропорцию:
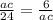
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

MN и ВС и секущей ОВ), а <MBO=<OBC (так как ОВ - биссектриса угла В треугольника АВС). Отсюда МВ=МО. Точно так же в треугольнике NOC имеем ON=NC. MN = MO+ON или MN=MB+NC. AB=AM+MB, AC=AN+NC. Тогда периметр треугольника AMN равен
АМ+AN+NO+OM = АМ+AN+NC+MB = АВ+АС, что и требовалось доказать.
б) Из прямоугольного треугольника АОР (радиус в точку касания перпендикулярен касательной) имеем: АР=√(AO²-OP²)=√(16r²-r²) = r√15. Тогда по свойству: "Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно d=(a+b-c)/2 = p-c", где с- сторона, лежащая против угла С, имеем: АВ+АС-ВС = 2r√15 (1).
С другой стороны по формуле площади треугольника имеем: Sabc=p*r, где р - полупериметр треугольника АВС. Отсюда r=S/p = 2√15/(AB+AC+BC). (2)
Подставляем (2) в (1): АВ+АС-ВС = 2*(2√15/(AB+AC+BC))*√15. ВС=2, тогда
АВ+АС-2 = 2*(2√15/(AB+AC+2))*√15. Или (АВ+АС-2 )*(AB+AC+2)=4*15. Или (АВ+АС)²-4=4*15, отсюда
(АВ+АС)=√(4(1+15))=8.Но выше мы доказали, что АВ+АС - это периметр треугольника AMN.
ответ: Pamn=8.