Question

Высота равнобокой трапеции равна 4√3 см, а тупой угол равен 120°. найдите площадь трапеции, если её диагональ делит острый угол трапеции пополам.

Answer 1

Равнобокая трапеция АВСД: АВ=СД, <В=<С=120°
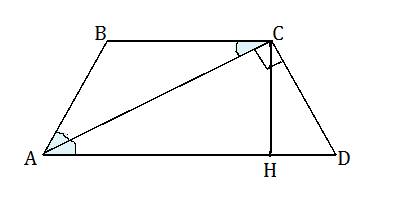
Значит  <А=<Д=180-120=60°
Высота трапеции ВН=4√3
Из прямоугольного ΔАВН:
АВ=ВН/sin A=4√3 / √3/2=8
AH=BH/tg A=4√3 / √3=4
Диагональ АС делит угол А пополам (<ВАС=<ДАС=60/2=30°).
В ΔАВС получается, что <ВАС=<ВСА, значит треугольник- равнобедренный (АВ=ВС=8)
АД=2АН+ВС=2*4+8=16
Площадь трапеции 
S=(АД+ВС)*ВН/2=(16+8)*4√3/2=48√3

Answer 2

Вариант решения.
Сумма углов, прилежащих к боковой стороне трапеции, равна 180°. 
∠ АВС=120°, ⇒ 
∠ ВАD=60°. 
АС- биссектриса и делит угол пополам. 
∠ САD=60°:2=30° 
СН - высота=4√3  
Высота равнобедренной трапеции, опущенная из вершины на большее основание, делит его на отрезки, один из которых равен полусумме оснований, а другой — полуразности оснований.  ⇒ 
 АН-полусумма оснований. 
АН=СН:tg 30°=4√3:(1/√3)=12 см 
Площадь трапеции равна произведению её высоты на полусумму оснований .
S=АН*СН=12*4√3=48 √3 см²
 --------------
 Можно АН найти и по т.Пифагора:
 АН = √(АС²-СН²), где СН=АС:2 как катет, противолежащий углу 30°