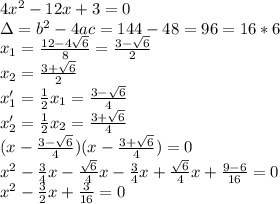
Доказательство:
Т.к. ABCD - параллелограмм, то AB//CD и AD//BC.
∠ECD = ∠CEB как накрест лежащие при параллельных прямых AB и CD и секущей EC.
∠EDC = ∠DEA как накрест лежащие при параллельных прямых AB и CD и секущей ED.
Т.к. EC = ED , то ΔECD - равнобедренный с основанием CD.
Значит ∠ECD = ∠EDC как углы при основании.
Следовательно ∠CEB = ∠DEA
ΔEBC = ΔEAD по двум сторонам и углу между ними (EB = EA по условию.)
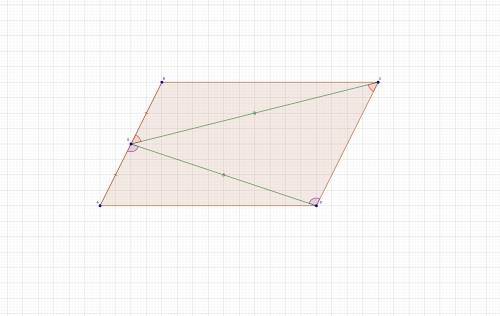
См. рисунок 2.
Из равенства треугольников EBC и EAD следует, что ∠EBC = ∠EAD
и ∠BCE = ∠ADE
∠BCD = ∠BCE + ∠ECD
∠ADC = ∠ADE + ∠EDC
Следовательно ∠BCD = ∠ADC
Продолжим сторону AD влево.
∠FAB = ∠ABC как накрест лежащие при параллельных прямых AD и BC и секущей AB.
∠FAB = ∠ADC как соответственные при параллельных прямых AB и DC и секущей AD
Собирая все вместе получаем, что ∠ABC = ∠BCD = ∠CDA = ∠DAB
Получается, что ABCD - параллелограмм в котором все углы равны. Следовательно ABCD - прямоугольник
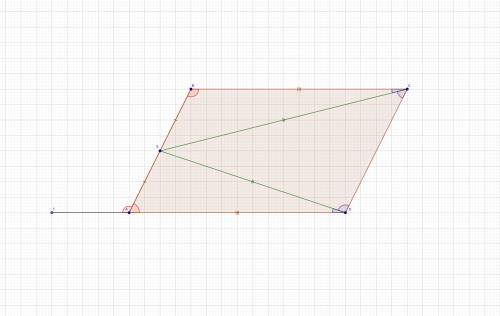
Теорема. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Доказательство. Пусть ABC – данный треугольник, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами. Прямоугольные треугольники AOD и AOE равны по гипотенузе и катету. У них гипотенуза AO общая, а катеты OD и OE равны как радиусы. Из равенства треугольников следует равенство углов OAD и OAE. А это значит, что точка O лежит на биссектрисе треугольника, проведённой из вершины A. Точно так же доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.
Объяснение: