Треугольник равнобедреный,это значит,что боковые стороны равны между собой и углы при основании треугольника тоже равны между собой
Рассмотрим Угол FDC,он равен 72 градуса,сумма всех углов треугольника СDF равна 180 градусов,углы при основании равны между собой и мы сейчас можем узнать чему равны угол F и угол С
(180-72):2=54 градуса
Из точки D на основание равнобедреного треугольника опущена DK- медиана,а по определению мы знаем,что если из вершины равнобедренного треугольника на основание треугольника опущена медиана,то она одновременно является и высотой,т е перпендикулярна основанию,и биссектрисой,т е делит угол пополам
Поэтому угол FDK=72:2=36 градусов
Так как как медиана в данном случае является и биссектрисой и высотой,то угол СКD=90 градусов,т к высота перпендикуляр к основанию FC ,и образовывает при основании два прямых угла по 90 градусов
Теперь найдём сторону FK
По условию,из вершины на основание опущена медиана,она по определению делит основание на две равные части
Основание равно 18 см
FK=18:2=9 см
Объяснение:
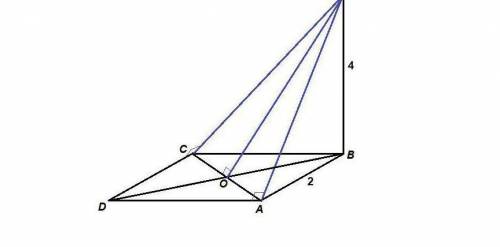
d(М, АВ) = d(M, BC) = 4 дм
d(M, AD) = d(M, СD) = 2√5 дм
d(M, BD) = 4 дм
d(M, AC) = 3√2 дм
Объяснение:
Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к этой прямой.
МВ - перпендикуляр к плоскости квадрата, а значит, и к любой прямой, лежащей в этой плоскости.
МВ⊥АВ, значит расстояние от точки М до прямой АВ
d(М, АВ) = МВ = 4 дм
МВ⊥ВС, значит
d(M, BC) = MB = 4 дм
МВ⊥BD, значит
d(M, BD) = MB = 4 дм
BA⊥AD как стороны квадрата,
ВА - проекция МА на плоскость, значит МА⊥AD по теореме о трех перпендикулярах, тогда
d(M, AD) = MA
Аналогично, ВС⊥CD как стороны квадрата, ВС - проекция МС на плоскость, значит МС⊥CD по теореме о трех перпендикулярах, тогда
d(M, СD) = MС
Если равны проекции наклонных, проведенных из одной точки, то равны и сами наклонные:
ВС = ВА (стороны квадрата), значит МС = МА.
Из прямоугольного треугольника АВМ по теореме Пифагора:
МА = √(АВ² + ВМ²) = √(4 + 16) = √20 = 2√5 дм
Итак,
d(M, AD) = d(M, СD) = 2√5 дм
Осталось найти расстояние от М до диагонали АС.
ВО⊥АС по свойству диагоналей квадрата,
ВО - проекция МО на плоскость квадрата, значит
МО⊥АС по теореме о трех перпендикулярах.
d(M, AC) = MO
BD = AB√2 =2√2 дм как диагональ квадрата,
BО = BD/2 = √2 дм (диагонали квадрата делятся точкой пересечения пополам)
Из прямоугольного треугольника МВО по теореме Пифагора:
МО = √(ВО² + ВМ²) = √(2 + 16) = √18 = 3√2 дм
d(M, AC) = 3√2 дм
ответ: 1 см