10 см.
Объяснение:
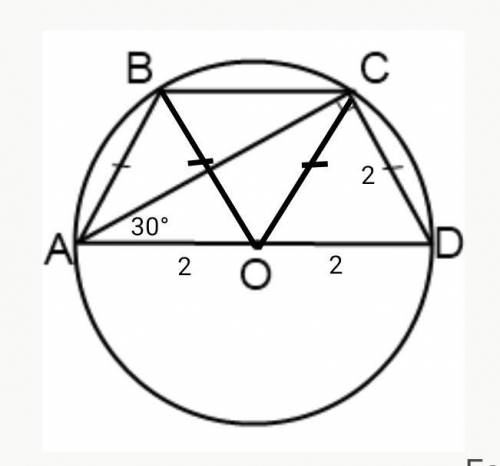
1. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. С другой стороны, сумма углов, прилежащих к боковой стороне трапеции, тоже равна 180°, тогда углы при основаниях трапеции равные, и отсюда следует, что вписать в окружность можно только равнобедренную трапецию. В нашем случае трапеция АВСD равнобедренная, АВ = СD = 2 см, ∠CAD = 30°.
2. Так как по условию центр описанной окружности лежит на большем основании, то ∠ АСD вписанный, опирающийся на диаметр, тогда по теореме ∠ АСD = 90°.
3. В прямоугольном треугольнике ACD напротив угла в 30° лежит катет, равный половине гипотенузы, тогда AD = 2•CD = 2•2 = 4 (см).
4. ∆ABO и ∆DCO равные равносторонние, все их углы по 60°, тогда и в равнобедренном ∆BOC ∠BOC = 180° - (60°+60°) = 60°, тогда и он равносторонний, ВС = ОВ = ОС = 2 см
5. Р ABCD = 4 + 2 + 2 + 2 = 10 (см)
10 см.
Объяснение:
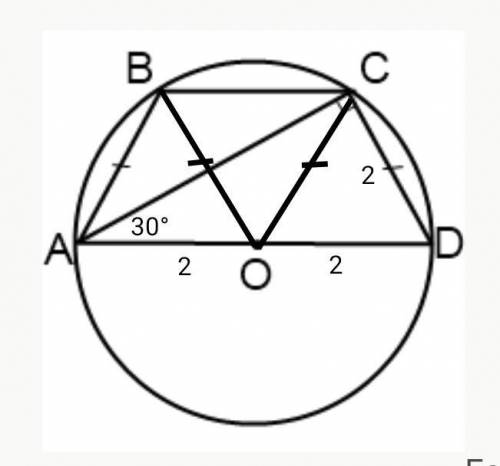
1. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. С другой стороны, сумма углов, прилежащих к боковой стороне трапеции, тоже равна 180°, тогда углы при основаниях трапеции равные, и отсюда следует, что вписать в окружность можно только равнобедренную трапецию. В нашем случае трапеция АВСD равнобедренная, АВ = СD = 2 см, ∠CAD = 30°.
2. Так как по условию центр описанной окружности лежит на большем основании, то ∠ АСD вписанный, опирающийся на диаметр, тогда по теореме ∠ АСD = 90°.
3. В прямоугольном треугольнике ACD напротив угла в 30° лежит катет, равный половине гипотенузы, тогда AD = 2•CD = 2•2 = 4 (см).
4. ∆ABO и ∆DCO равные равносторонние, всё их углы по 60°, тогда и в равнобедренном ∆BOC ∠BOC = 180° - (60°+60°) = 60°, тогда и он равносторонний, ВС = ОВ = ОС = 2 см
5. Р ABCD = 4 + 2 + 2 + 2 = 10 (см)
диагонали АС=ВД=√(а²+b²)=√(36+64)=√100=10.
Окружность с центром О и радиусом ОА=ОД=АД/2=4 пересекает диагональ АC в точке К.
Получается, что АС- секущая окружности, а СД - касательная к окружности, проведенные из одной точки С.
Значит СД²=АС*КС
КС=СД²/АС=36/10=3,6
АК=АС-КС=10-3,6=6,4
ответ: 6,4 и 3,6