


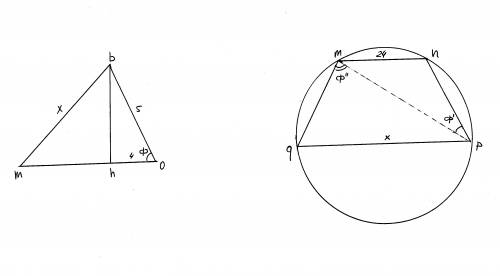
1). см левый рисунок на чертеже.
По теореме синусов x = 2*R*sin(Ф); sin(Ф) вычисляется из треугольника bho, который, очевидно, "египетский" (3,4,5) :))) то есть sin(Ф) = 3/5; x = 2*10*3/5 = 12;
2). см. правый рисунок на чертеже.
Я отметил углы, которые принял за заданные: sin(Ф') = 0,2; cos(Ф") = 0,6; (конечно, таким я себе жизнь облегчил, но тут уж все - к автору задачи :)))
Имеем cos(Ф") = 0,6; откуда sin(Ф") = 0,8;
Поскольку у треугольников mqp и mnp общая описанная окружность, из теоремы синусов следует
x/0,8 = 24/0,2;
отсюда x = 96, а средняя линяя равна (96 + 24)/2 = 60;
Пусть дана прямоугольная трапеция ABCD. у которой ВС и AD - основания, угол А =углу В=90 градусов. О- центр вписанной в трапецию окружности, точка М - точка касания окружности стороны AD и точка К - точка касания окружности стороны ВС. АМ=20 см, MD=25 см, тогда ОМ=ОК=r=20см и АВ=40 см. DM=DK=25 см как отрезки касательных,проведенных из одной точки. Угол С+ угол D трапеции=180 градусов, как внутренние накрест лежащие углы, DO и CO - биссектрисы соответствующих углов, то угол CDO+DCO=90градусов, следовательно угол COD=90 градусов, т.е. треугольник COD - прямоугольный, у которого ОК - высота, проведенная к гипотенузе, OK^2=DK*CK, CK=400/25=16 см. Значит периметр трапеции равен 20+25+25+16+16+20+40=162 см
ответ: Р=162 см