Объяснение:
Дано:
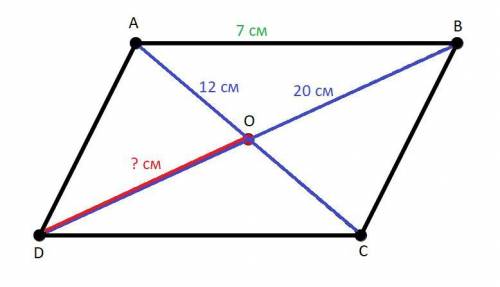
ABCD - параллелограмм.
AC и BD - диагонали параллелограмма.
AC ∩ BD = O.
AC = 12 (см); BD = 20 (см); AB = 7 (см).
Найти:
DO - ? (см).
Тут всё довольно просто. Так как ABCD - параллелограмм, вспомним свойство такой геометрической фигуры: диагонали параллелограмма точкой пересечения делятся пополам. Т.е. диагонали AC и BD делятся точкой пересечения O пополам. Соответственно DO будет равняться половине всей диагонали BD. (и из этого следует, что DO = OB)
DO = BD/2 = 20 : 2 = 10 (см)
S =S(ABCD) -?
S =AB*BC*sin<ABC =AB² *sinα .
1+tq²α =1/cos²α ;
cosα =1/√(1+tq²α) * * * 0<α<90° * * *
cosα =1/√(1+15) =1/4 ⇒sinα =tqα*cosα =(√15 ) /4 .
Из ΔABC по теореме косинусов:
AC² =AB² +BC² -2AB*BC*cosα =2AB²(1-cosα)⇒AB² =AC²/2(1-cosα) =4²/2(1-1/4) =32/3 .
S = AB² *sinα =32/3* √15 ) /4 = (8√15)/3 .