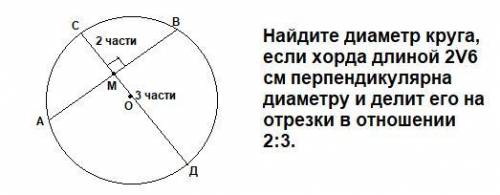
Найдите диаметр круга, если хорда длиной 2V6 см перпендикулярна диаметру и делит его на отрезки в отношении 2:3.
Объяснение:
ΔОМА=ΔОМВ как прямоугольные по двум катетам ОМ-общий, ОА=ОВ как катеты ⇒МА=МВ=2√6:2=√6 (см)
По т. об отрезках пересекающихся хорд АМ*МВ=СМ*МД
Т.к. СМ/МД=2/3 , то МД=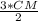 
. Получим √6*√6= СМ* .
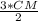СМ²=4, СМ=2 см .
Тогда МД=3 см , поэтому диаметр равен d= СМ+МД=2+3=5 (см).
d=5 см
=====================
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
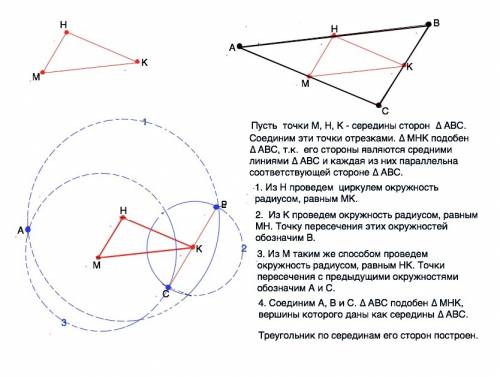
Пусть точки М, Н, К - середины сторон ∆ АВС.
Соединим эти точки отрезками. ∆ МНК подобен ∆ АВС, т.к. его стороны являются средними линиями ∆ АВС и каждая из них параллельна соответствующей стороне ∆ АВС.
1. Из Н проведем циркулем окружность 1 радиусом, равным МК.
2. Из К проведем окружность 2 радиусом, равным МН. Точку пересечения этих окружностей обозначим В.
3. Из М таким же проведем окружность 3 радиусом, равным НК. Точки пересечения с предыдущими окружностями обозначим А и С.
4. Соединим А, В и С. ∆ АВС подобен ∆ МНК, вершины которого даны как середины ∆ АВС.
Построение треугольника по серединам сторон готово.
Трапеция АВСD - четырехугольник. ⇒
АD+BC=AB+CD
АD+BC=20
AB+CD=20
Пусть АВ=х.
Тогда
CD=20-x⇒
Опустим из С высоту на большее основание и получим треугольник СНD,
в котором НD=12-8=4
CH=AB=x
CD=20-x
По т.Пифагора
НD²=CD²=CH²
16=400-40x+x²-x²
40x=384
x=9,6
Высота трапеции равна диаметру вписанной в нее окружности.
D=9,6
r=9,6:2=4,8