ответ: 6√3 см²
Объяснение:
Вариант решения.
Медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины. Как следствие из этого свойства: площадь треугольника делится медианами на 6 равных частей.
Если провести третью медиану АК, получим 6 равновеликих треугольников с общей вершиной О.
Ѕ(ВОК)=Ѕ(СОК) ⇒ Ѕ(АВС)=6•(ЅВОК)=3•Ѕ{ВОС)
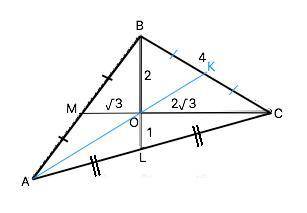
На приложенном рисунке обозначим длины частей медиан.
Ѕ{ВОС)=ВО•СО•ѕin(BOC)
По т.косинусов соѕВОС = 0 ( проверьте вычисления). Это косинус 90⇒
треугольник ВОС – прямоугольный ( что подтверждает и проверка по т.Пифагора).⇒
Ѕ(АВС)=3•0,5•ВО•ОС=3•0,5•4√3=6√3 см²
Если двугранные углы при основании пирамиды равны, то высота пирамиды проецируется в центр окружности, вписанной в основание - точку О, и высоты боковых граней равны.
Сначала выразим в основании все нужные величины:
АН : ВН = ctg (α/2) ⇒ AH = BH · ctg(α/2) = 
BH : AB = sin(α/2) ⇒ AB = BH / sin(α/2) = 
Pabc = 2AB + BC = a/sin(α/2) + a
Sabc = 1/2 · BC · AH = 1/2 · a · a/2 · ctg(α/2) = a²/4 · ctg(α/2)
r = 2Sabc / Pabc
r = 2· a²/4 · ctg(α/2) / (a/sin(α/2) + a) = a·cos(α/2) / (2 + 2sin(α/2))
ΔSOH:
OH : SH = cosβ ⇒ SH = OH / cosβ = r / cosβ = 2Sabc / (Pabc · cosβ)
Теперь площадь полной поверхности:
S = Sбок + Sосн = 1/2 · Pabc · SH + Sabc
S = 1/2 · Pabc · 2Sabc / (Pabc · cosβ) + Sabc
S = Sabc/cosβ + Sabc = Sabc · (1/cosβ + 1)
S = a²/4 · ctg(α/2) · (1/cosβ + 1)
Вообще, если боковые грани наклонены под одним углом к основанию
Sосн /Sбок = cosβ
Высота пирамиды:
ΔSOH:
SO / r = tgβ
SO = r · tgβ = a·cos(α/2) · tgβ / (2 + 2sin(α/2))