Построим координатный параллелепипед точки А. Отметим на оси х — Ах(1;0;0); у — Ау(0;2;0); z — Аz (0;0;3).
Затем из точки Ах проведем две прямые, параллельную оси у и оси z, из точки Ау — прямые параллельные оси x и оси z; из Аz — параллельные оси х и оси у.
При пересечении прямых получаются точки Аху, Ауz, Ахz. Тогда
AxAxy = 2; AxAxz = 3; AyAxy = 1; AyAyz = 3; AzAxz = 1; AzAyz = 2;
Перпендикулярами на координатные оси будут отрезки ААz ААу; АAх на координатные плоскости αху, Ауz АХz. Получаем что основания перпендикуляров: Аху(1;2;0), Аyz(0;2;3), Аxz(1;0;3).ответ:
Объяснение:
 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 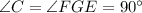 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 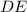 , то
, то 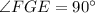 ).
).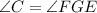 и
и 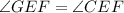 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: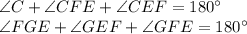
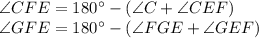
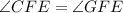 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: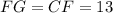
 . Смотрите второй рисунок.
. Смотрите второй рисунок.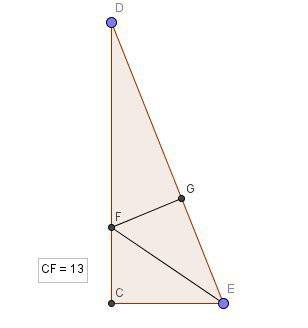
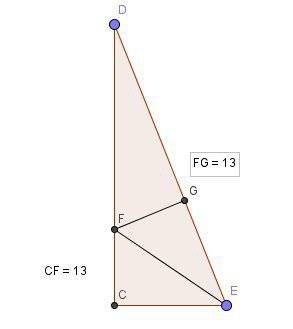
Проведём высоты BF и CG.FG = BC = 8 смПоскольку трапеция равнобедренная, AF = GD = (AD - FG)/2 = (10 - 8)/2 = 1 см.AG = AD - AF = 10 - 1 = 9 см. CG -- высота, опущенная на гипотенузу. Поэтому: CG² = AG·GD = 9·1 = 9 см².CG = BF = 3 смПо теореме Пифагора: AC² = AG² + CG² = 9² + 3² = 90 см²AC = √90 = 3√10 смΔACG ~ ΔCBE по двум углам, поэтому AC : BC = AG : EC.3√10 : 8 = 9 : ECEC = 72 / 3√10 = 24/√10 = 2,4√10 смAE = AC - EC = 3√10 - 2,4√10 = 0,6√10 смAE : EC = 0,6√10 : 2,4√10 = 1 : 4.