Доброго времени суток!
Как я поняла, вопрос был поставлен таков : "Стороны равнобедренного треугольника пропорциональны числам 1, 1, √2. Докажите, что этот треугольник — прямоугольный".
если это не так, то сообщите об этом в комментариях.
▔ ▔ ▔
★☆★ Чертёж смотрите во вложении ★☆★
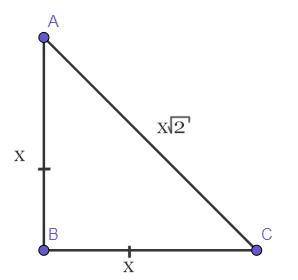
Дано:ΔАВС — равнобедренный (АВ = ВС).
АВ : ВС : АС = 1 : 1 : √2.
Доказать:ΔАВС — прямоугольный.
Доказательство:▸Теорема, обратная теореме Пифагора — если квадрат большей стороны треугольника равен сумме квадратов других сторон, то такой треугольник — прямоугольный◂
Итак, пусть АВ = ВС = х, тогда, по условию задачи, АС = х√2.
Составим уравнение и проверим его на верность —
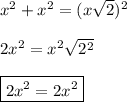
Итак, мы выяснили, что сумма квадратов меньших сторон равна квадрату большей стороны. Поэтому, по обратной теореме Пифагора, равнобедренный ΔАВС — прямоугольный.
ответ:что требовалось доказать.
проекции наклонных НВ=7 и НС=17
Из прямоугольного ΔАВН:
АН²=АВ²-НВ²=х²-7²=х²-49
Из прямоугольного ΔАСН:
АН²=АС²-НС²=(х+6)²-17²=х²+12х+36-289=х²+12х-253
Приравниваем:
х²-49=х²+12х-253
61х=253
х=253/61=4 9/61≈4,15 это АВ
АС=4 9/61+6=10 9/61≈10,15