Если в равнобедренной трапеции провести высоты ВН и СК, то получим НВСК - прямоугольник (ВС║КН, так как основания трапеции параллельны, ВН║СК как перпендикуляры к одной прямой), тогда
ВС = КН и ВН = СК.
ΔАВН = ΔDCK по гипотенузе и катету (АВ = CD, так как трапеция равнобедренная, ВН = СК), тогда
АН = DK = (AD - KH)/2 = (AD - BC)/2.
Площадь трапеции:
Sabcd = (AD + BC)/2 · BH
Воспользуемся этими выводами для решения задач:
а) AH = DK = (17 - 11)/2 = 3 см
ΔАВН прямоугольный с гипотенузой, равной 5 см и катетом 3 см, значит он египетский и
ВН = 4 см.
Sabcd = (17 + 11)/2 · 4 = 28/2 · 4 = 14 · 4 = 56 см²
б) AH = DK = (8 - 2)/2 = 3 см
ΔABH: ∠AHB = 90°, ∠BAH = 60°, ⇒ ∠ABH = 30°.
AB = 2AH = 6 см по свойству катета, лежащего напротив угла в 30°,
по теореме Пифагора:
BH = √(AB² - AH²) = √(36 - 9) = √27 = 3√3 см
Sabcd = (8 + 2)/2 · 3√3 = 15√3 см²
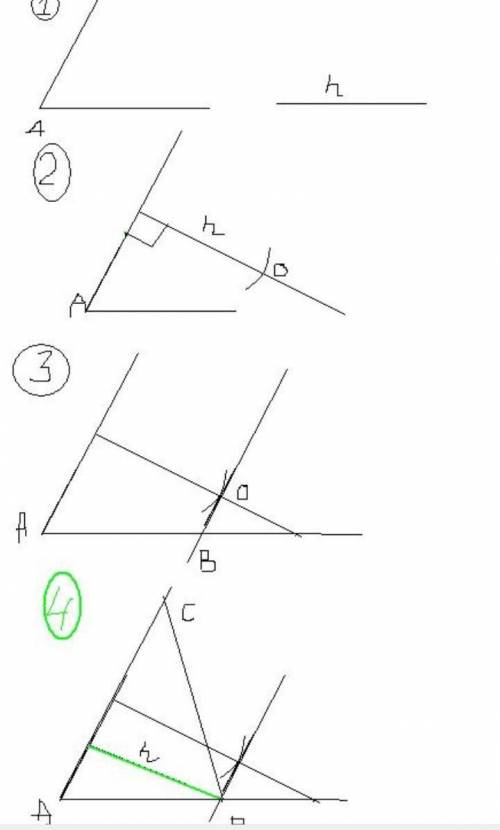
См. вложение.
1 дано угол и выстоа
2 Обозначим вершину данного угла буквой А. Строишь перпендикуляр к стороне в любом месте. На перпендикуляре откладываешь высоту. Получилась точка О.
3 Через нее, через точку О то есть, строишь еще один перпендикуляр, чтоб получилась линия параллельная боковой стороне. На ее пересечении с основанием находишь точку В.
4 В точке В строишь заданный угол, только в другую сторону и на пересечении линий находишь точку С. Три точки есть, треугольник построен. Можно проверить длину полученной высоты, показанна зелённым.
Так как мы знаем что периметр это сумма всех сторон надо найти все стороны.
1) 2+3+5+8=18 (частей) в 56 см
2) 56/18=3 1/9(3 целых одна девятая) (см) в 1 части
3) 3 1/9 * 2 = 6 2/9 (см) одна боковая сторона
4)3 1/9 * 3 = 9 1/3 (см) вторая сторона
5) 3 1/9 * 5 = 15 5/9 (см) третья сторона
6) 3 1/9 * 8 = 24 8/9 (см)