∠АВС = 80°.
Объяснение:
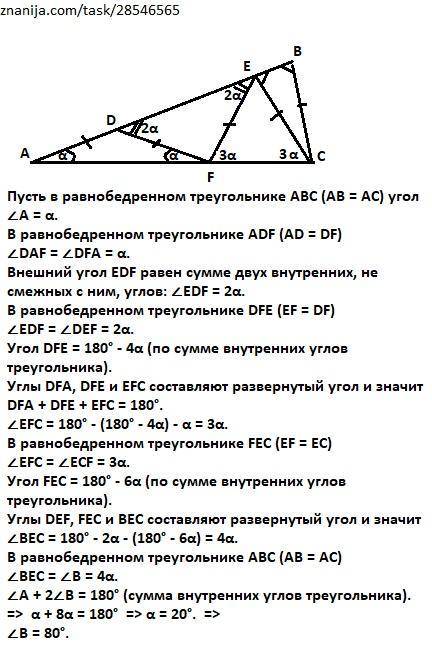
Пусть в равнобедренном треугольнике АВС (АВ = АС) угол
∠А = α.
В равнобедренном треугольнике ADF (AD = DF)
∠DAF = ∠DFA = α.
Внешний угол EDF равен сумме двух внутренних, не смежных с ним, углов: ∠EDF = 2α.
В равнобедренном треугольнике DFЕ (EF = DF)
∠EDF = ∠DEF = 2α.
Угол DFE = 180° - 4α (по сумме внутренних углов треугольника).
Углы DFA, DFE и EFС составляют развернутый угол и значит
DFA + DFE + EFС = 180°.
∠EFC = 180° - (180° - 4α) - α = 3α.
В равнобедренном треугольнике FЕС (EF = ЕС)
∠EFС = ∠EСF = 3α.
Угол FEС = 180° - 6α (по сумме внутренних углов треугольника).
Углы DЕF, FEC и BEC составляют развернутый угол и значит
∠ВЕС = 180° - 2α - (180° - 6α) = 4α.
В равнобедренном треугольнике АВС (АВ = АС)
∠ВЕС = ∠В = 4α.
∠А + 2∠В = 180° (сумма внутренних углов треугольника). => α + 8α = 180° => α = 20°. =>
∠В = 80°.
B1. ↑MN (- 4 ; 3 )
|↑MN| = √((-4)² + 3²) = √(16 + 9) = √25 = 5
B2. А( 2 ; 0 ), В( - 1 ; 3 ), С( 4 ; 6 )
↑BA = {2 - (- 1) ; 0 - 3} = {3 ; - 3}
↑BC = {4 - (-1) ; 6 - 3} = {5 ; 3}
↑a = ↑BA - ↑BC = {3 - 5 ; - 3 - 3} = {- 2 ; - 6}
B3. A( 2 ; 3 ) С( 2 ; 1 ) - середина отрезка АВ.
B( x ; y)
Координаты середины отрезка равны полусумме соответствующих координат:
2 = (2 + х)/2
x + 2 = 4
x = 2
1 = (3 + y)/2
y + 3 = 2
y = - 1
B( 2 ; - 1 )
B4. А( 1 ; 4 ) B( - 3 ; 7 )
АВ - диаметр окружности,
O( х ; у ) - центр окружности, т.е. середина отрезка АВ.
x = (1 + (- 3))/2 = - 1
y = (4 + 7)/2 = 11/2 = 5,5
O( - 1 ; 5,5 )
B5. А( 2 ; - 5 ) и В( 1 ; 6 )
↑AB = ↑CA
Пусть С( х ; у )
↑AB = {1 - 2 ; 6 - (- 5)} = {- 1 ; 11}
↑CA = {2 - x ; - 5 - y}
Так как векторы равны, координаты их так же равны:
2 - x = - 1
x = 3
- 5 - y = 11
y = -16
C( 3 ; - 16 )
B6. A( 2 ; 6 ) и В( 4 ; 8 )
AB = √((2 - 4)² + (6 - 8)²) = √(4 + 4) = √8 = 2√2