Треугольник АВС отображается в треугольник А'В'С' с параллельного переноса. Известно, что В (-3;5), С(-5;1), А'(-3;-2), С'(-1;-3). Определите координаты остальных вершин треугольников.
Объяснение:
При параллельном переносе точки А-->А'(-3;-2) ,В(-3; 5)-->B',
С(-5;1)--->С'(-1;-3).
Ищем вектор параллельного переноса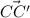 
(-1 +5;-3 -1) или 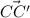(4;-4)
1) Тогда х(АА')=х(А')-х(А) , 4=-3-х(А) , х(А)=-7,
у(АА')=у(А')-у(А) , -4=-2-у(А) , у(А)=2, А'( -7; 2).
2) Для точек В(-3; 5)-->B' имеем х(ВВ')=х(В')-х(В) , 4=х(В')+3 , х(В')=1 ,
у(ВВ')=у(В')-у(В) , -4=у(В')-5 , у(В')=1, В'( 1; 1).
orjabinina
Так как окружность является описанной около треугольника , то его гипотенуза является диаметром . . Пусть одна часть равна х, тогда гипотенуза равна 5х, катет 3х, получим уравнение (5 х) в квадрате = 16 в квадрате + ( 3х)в квадрате - по теореме Пифагора.
Получаем 25 х в квадрате = 256 + 9х в квадрате.
16 х в квадрате = 256
х в квадрате = 16
х= 4 ; х= -4
-4 не удовлетворяет условию задачи.
Найдём гипотенузу 5х= 5*4 = 20, гипотенуза это диаметр, значит радиус 20:2 =10
ответ : 10 см
