Объяснение:
так думаю.
Точка пересечения серединных перпендикуляров треугольника равноудалена от его вершин. Значит любая точка, лежащая на перпендикуляре, проведенном из точки пересечения серединных перпендикуляров, тоже равноудалена от вершин треугольника (равенство треугольников, образованных серединными перпендикулярами и общей стороной - перпендикуляром, т. е. по двум сторонам и углу между ними) .
Может теорема такая?
Точка равноудалена от сторон треугольника, если это точка принадлежит перпендикуляру, проведенному из точки пересечения серединных перпендикуляров треугольника. Может так звучит?
нравится8
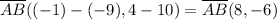 ;
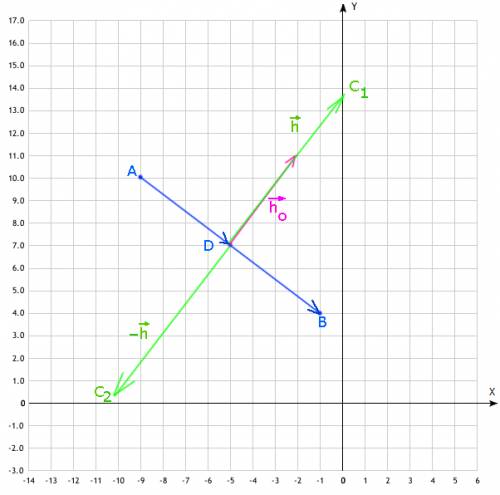
; от точки A
от точки A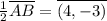 ;
; в обе возможные стороны
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: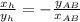 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 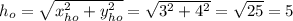 ;
;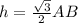 , т.к
, т.к 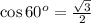 ;
;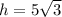 , а стало быть
, а стало быть  ;
;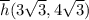 .
.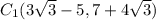 /// примечание:
/// примечание: 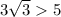 ;
;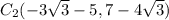 /// примечание:
/// примечание: 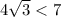 .
.
ширина 12см
(10+12)×2
24×2=48