∠DKC = 24°.
Объяснение:
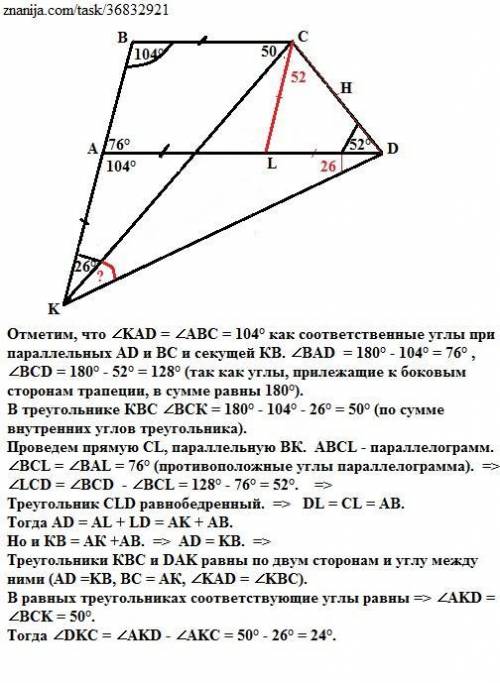
Отметим, что ∠KAD = ∠ABC = 104° как соответственные углы при параллельных AD и ВС и секущей КВ.
∠BAD = 180° - 104° = 76° , ∠BCD = 180° - 52° = 128° (так как углы, прилежащие к боковым сторонам трапеции, в сумме равны 180°).
В треугольнике КВС ∠ВСК = 180° - 104° - 26° = 50° (по сумме внутренних углов треугольника).
Проведем прямую СL, параллельную ВК.
АВСL - параллелограмм.
∠BCL = ∠BAL = 76° (противоположные углы параллелограмма). =>
∠LСD = ∠BCD - ∠BCL = 128° - 76° = 52°. =>
Треугольник СLD равнобедренный. => DL = CL = AB.
Тогда AD = AL + LD = AK + AB.
Но и КВ = АК +AВ. => AD = KB. =>
Треугольники КВС и DAK равны по двум сторонам и углу между ними (AD =KB, BC = АК, ∠KAD = ∠KBC).
В равных треугольниках соответствующие углы равны => ∠AKD = ∠BCK = 50°.
Тогда ∠DKC = ∠AKD - ∠AKC = 50° - 26° = 24°.
∠DKC = 24°.
Объяснение:
Отметим, что ∠KAD = ∠ABC = 104° как соответственные углы при параллельных AD и ВС и секущей КВ.
∠BAD = 180° - 104° = 76° , ∠BCD = 180° - 52° = 128° (так как углы, прилежащие к боковым сторонам трапеции, в сумме равны 180°).
В треугольнике КВС ∠ВСК = 180° - 104° - 26° = 50° (по сумме внутренних углов треугольника).
Проведем прямую СL, параллельную ВК.
АВСL - параллелограмм.
∠BCL = ∠BAL = 76° (противоположные углы параллелограмма). =>
∠LСD = ∠BCD - ∠BCL = 128° - 76° = 52°. =>
Треугольник СLD равнобедренный. => DL = CL = AB.
Тогда AD = AL + LD = AK + AB.
Но и КВ = АК +AВ. => AD = KB. =>
Треугольники КВС и DAK равны по двум сторонам и углу между ними (AD =KB, BC = АК, ∠KAD = ∠KBC).
В равных треугольниках соответствующие углы равны => ∠AKD = ∠BCK = 50°.
Тогда ∠DKC = ∠AKD - ∠AKC = 50° - 26° = 24°.

сначала найди радиус: R=abc/4 корня квадратных из p(p-a)*(p-b)*(p-c)
полупериметр - = 1/2*( 5+4+3)=6
радиус 5*4*3/4 корня квадратных из (6*1*2*3)=60/4 корня из 36=60/24=2,5см
Чертим окружность, а потом заданные стороны. Вершины лежат на окружности