.............................
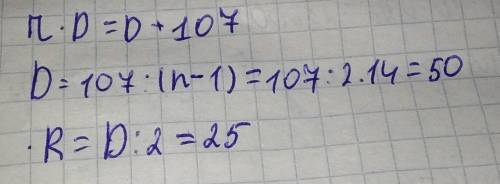
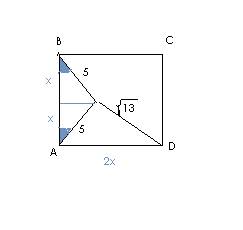
Делаем рисунок к задаче.
Найдя второй угол при основании bc, обнаружим, что треугольник аbc - равнобедренный. А треугольник асh- половина равностороннего треугольника и аh в нем можно найти по формуле высоты равностороннего треугольника ( по теореме Пифагора получим тот же результат).
Найдем bc=2 аh=ас√3
Искомые отношения сторон равны, поэтому
ас:bc=аb:bc=√3 :2 или ½√3
(в решении, данном во вложенном рисунке, опечатка, читаем ас:bc=аb:bc=√3)
---------------------------
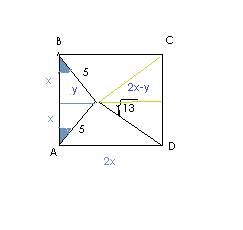
Принцип решения второго задания совершенно такой же. Решение во втором рисунке.
Объяснение:

Решение.
Обозначим длину окружности как C, а диаметр как D.
Таким образом C - D = 107
Длина окружности равна С = 2πR = πD , поэтому
πD - D = 107
D ( π - 1 ) = 107
D = 107 / ( π - 1 ) ≈ 49,96 см
Откуда радиус окружности R = D / 2 = 107 / 2( π - 1 ) ≈ 24,98 см
ответ: 107 / 2( π - 1 ) ≈ 24,98 см