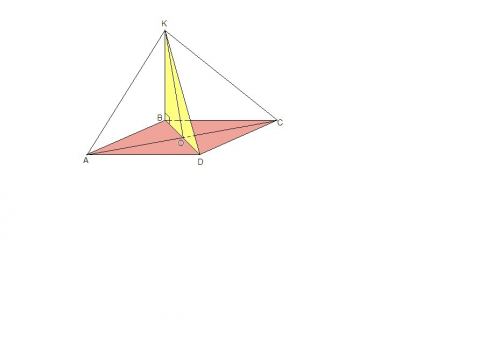
Докажем, что АВСD - трапеция с основаниями
Рассмотрим треугольники ВСО и АDO. Они подобны по второму признаку: угол ВОС=углу АОD (как вертикальные), АО/ОС=18/12=1,5 и ВО/OD=15/10=1,5.
У подобных фигур соответствующие углы равны, т.е. угол СВО=углу ОDA и угол ВСО=углу ОАD. В то же время углы СВО и ОDA являются внутренними накрест лежащими при секущей ВD и прямых ВС и AD, следовательно, ВС || AD.
Аналогично, углы ВСО и ОАD являются внутренними накрест лежащими при секущей АС и прямых ВС и AD, следовательно, ВС || AD.
По определению трапеция - четырёхугольник, у которого две противоположные стороны параллельны, а две другие непараллельны. Так как ВС || AD, то АВСD - трапеция, что и требовалось доказать.
скалярное произведению этих векторов делить на произведение длин.
Скалярное произведение равно сумме произведений одноименных координат
Длина вектора равна корню квадратному из суммы квадратов координат
|a|=√((-1)²+2²)= √5,
|b|=√(3²+1²)=√10
ответ. косинус угла между векторами равен
-1/(5√2)