Не знаю, как здесь обозначить вектор. Пусть будет ⁻. То есть, а⁻ - вектор а.
a⁻ (-5; -10); b⁻ (2; 7).
1) a⁻ + b⁻ (-3; -3)
2) 4 · a⁻ (-20; -40)
3) -2 · a⁻ + 3 · b⁻ (16; 41)
4) -b⁻ (-2; -7)
p⁻ (-3; 4); l⁻ (1; 2)
1) p⁻ - l⁻ (-4; 2)
2) Признак коллинеарности векторов: векторы коллинеарны, когда их координаты пропорциональны. Проверяем, вектор (p⁻ - l⁻) имеет координаты (-4; 2), а вектор k - координаты (4; -2).
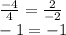
Так как их координаты пропорциональны, то эти векторы коллинеарны.
Если А (-2; 2), B (3; 5), то AB⁻ (5; 3).
∠1 = 60°; ∠2= 120°; ∠3 = 60°; ∠4= 120°.
Объяснение:
Задание
Найдите углы ромба ABCD, если его сторона равна 6 см, а большая диагональ 6√3 см.
Решение
Для решения задачи воспользуемся следующими свойствами диагоналей ромба:
1) диагонали ромба в точке пересечения делятся пополам;
2) диагонали ромба пересекаются под углом 90°;
3) диагонали ромба являются биссектрисами его углов.
1) В прямоугольном треугольнике, образованном пересечением диагоналей и стороной ромба:
- сторона ромба (6 см) является гипотенузой;
- половина большей диагонали (6√3 : 2 = 3√3 см) катетом.
2) Рассчитаем косинус угла α образованного стороной ромба и большей диагональю:
cos α = 3√3 / 6 = √3/2,
α = arccos √3/2 = 30°.
3) ∠1 = 2α = 30° · 2 = 60°.
4) Так как сумма углов ромба, прилежащих к одной стороне, равна 180°, то ∠2 = 180 - 60 = 120 °.
5) Противоположные углы ромба равны:
∠3 =∠1 = 60°.
∠4 =∠2= 120°.
ответ: ∠1 = 60°; ∠2= 120°; ∠3 = 60°; ∠4= 120°.