а) Доказательство:
По теореме о сумме углов в треугольнике:
∠С = 180° - ∠A - ∠B = 180° - 40° - 100° = 40°.
Если ∠С = 40°, то ∠С = ∠A. Из этого следует, что △ABC - равнобедренный (BA = BC), что и требовалось доказать.
б) Решение:
Выше мы уже доказали, что △ABC - равнобедренный (BA = BC).
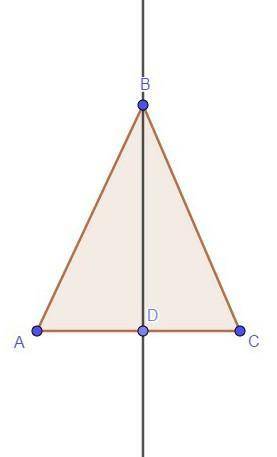
В равнобедренном треугольнике высота, проведённая из вершины угла, противоположного основанию (в данном случае из ∠B), является также его биссектрисой.
Биссектриса делит угол пополам. Отсюда ∠ABH = ∠CBH. А если ∠B = 100°, то ∠ABH = ∠CBH = 100° / 2 = 50°.
ответ: 50°.
Если сумма оснований трапеции равна сумме боковых сторон, то в нее можна вписать окружность. В нашем случае а+b=с+d, с=d, а+b=2с. Р=а+b+с+d=а+b+2с, Р=4с, 100=4с, с=25 см. S=(a+b)/2*корень с (c2-((b-a)^2+c^2-d^2)/(2*(b-a)))^2), 600=50/2*корень с (625-((b-a)/2)^2), 24=корень с (625-(b-a)/2)^2), 576=625-((b-a)/2)^2, 49=(b-a)^2/4, 196=(b-a)^2, 14=b-a, b=14+a. a+a+14=2c, 2a+14=2c, 2a+14=50, 2a=36, a=18 см, b=14+18=32 см.