1) дано угол В=30 градусов ВА=4 см
решение
проведем АС перпендикуляр к прямой а угол ВСА=90 градусов
получим прямоугольный треугольник АВС
пусть АС=х тогда по свойству что против угла в 30 градусов лежит катет равный половине гипотинузы х=ВА\2
значит АС= 2 см ответ 2 см
2) дано: треугольник АВС равнобедренный (так как угли при основании равны) ВС=14см
проведем АР
т.к. АВС равнобедренный то АР высота медиана биссектриса
значит ВР=СР=14\2=7см
треугольник арс прямоугольный и равнобедренный т.к. угол рас =180-90-45=45 градусов
значит ар=7см
3) тут не дано ни одной величины
это треугольник прямоугольный т.к. 180-30-60=90
значит катет лежащий против угла в 30 градсов равен половине гипотинузы следовательно ас=х тогда вс=2х
тогда ва^2=4х^2-x^2
ва=х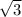
если провести высоты ар то получим новый прямоугольный треугольник вра в котором ар=(х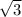 )\2
)\2
Объяснение:
5 номер
В равнобедренном треугольнике две стороны равны.
По неравенству сторон треугольника знаем, что сумма двух сторон треугольника не может быть меньше третьей.
Предположим, что третья сторона равна 4 см.
Проверим, 4+4<9 - не подходит.
9+9>4 - подходит, значит, третья сторона = 9 см
6 номер
1)Рассмотрим треугольник DME:
предположим ,что угол DME - тупой (будет смежным с острым углом этого треугольника) и
угол DEM - острый (так как двух углов тупых не может быть в треугольнике по определению и признаку треугольника) .
2)Если напротив большего угла в данном треугольнике лежит самая большая сторона,то DE>DM.
7 номер
<B = 180° - (79°+ 55°)= 46° .
<C = 180° - ( 46° + 55°) = 79° .
< А = 55° (по условию).
6х=30см
х=5см
Одна сторона = 5 см
Вторая = 5*2 = 10 см